
~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) $6-\dfrac25-\dfrac85$
こたえ
前から順番に引き算を行ってもよいのですが,6から引く数の合計に着目してみましょう。$\dfrac25$ と $\dfrac85$ の2つを引くのですから,合計すると $\dfrac25+\dfrac85=\dfrac{10}5$,つまり2になります。これを6から引くのですから 6-2=4
答えは 4
(2) $6.23\times 0.001\times10000$
こたえ
かけ算はかける順番は好きな順でよいのです。ならば $0.001\times10000$ を先にするべきでしょう。$0.001\times10000=10$。よって $6.23\times10=62.3$
答えは 62.3
(3) $199.2\div24$
こたえ

答えは 8.3
(4) $12\div(5+2\times0.5)$
こたえ
カッコの中が先で,その中でもかけ算が優先ですから,$2\times0.5=1$。そして $5+1=6$。よって $12\div6=2$。
答えは 2
2 AからEの5人のグループで,だれが班長になるかをくじ引きで決めました。5人は次のように発言しましたが,本当のことを言っているのは1人だけでした。誰が班長になりましたか。
A「Dさんが班長になった。」
B「私が班長よ。」
C「ぼくは班長にならなかった。」
D「Aさんはうそをついているわ。」
E「Bさんが班長になった。」
10点
こたえ
Dさんの発言に注目してみます。
[1] Dさんだけが本当のことを話しているとき
Dさん以外のA,B,C,Eさんはみんなウソを言っていますから
A→Dは班長ではない。
B→Bは班長ではない
C→Cは班長である。
E→Bは班長ではない。
となります。よってこのときCさんが班長です。
Dさんの発言に注目してみます。
[2] Dさんがうそをついているとき
Dの発言から本当のことを話しているのはAだけで,あとのひとはみんなウソを言っています。
A→Dは班長である。
B→Bは班長ではない。
C→Cは班長である。
E→Bは班長ではない。
するとDとCが共に班長になってしまうので,この場合は正しくありません。
以上により,班長になったのは Cさん
3 ある日あいさんはデパートの6階に行くために,1階からエレベーターに乗りました。最初はあいさん1人でした。途中2階で何人か乗ってきました。そのあと3階を通過して4階についたとき,何人か降りたあと,新しく乗ってきた人はおらず,エレベーターに残った人はあいさんをふくめて6人でした。5階に着いたときは何人か降りましたが同時に何人か乗ってきました。6階に着いたときエレベーターに乗っていたのはあいさんをふくめて2人でした。
次の問いに答えなさい。ただしエレベーターの定員は10人とします。
10点×3=30(点)
(1) 2階で乗ってきた人は何人以上何人以下ですか。
こたえ
4階で何人か降りて,残った人が6人いたのですから,4階に到着するときには7人以上いたということになります。ということは、2階で乗ってきたのはあいさんをのぞく6人以上です。エレベーターの定員が10人ですから,2階ではあいさんをのぞくと残り9人まで乗れます。
答えは 6人以上9人以下
(2) 5階で降りた人数と乗ってきた人数はそれぞれ何人ですか。
こたえ
5階で何人か乗ってきて2人ということは,結局乗ってきたのは1人だけです。4階を出発したとき6人いたのですから,5階ではまず5人が降りてあいさん1人だけになり,そのあと1人が乗ってきたとわかります。
答えは 5人が降りて,1人が乗った
(3) あいさんが載ってから6階に着くまでにエレベーターを利用した人の,のべ人数として考えられるのは何人以上何人以下ですか。
こたえ
1階ではあいさん1人
2階では新たに6人以上9人以下の人が利用
4階では新しい利用客はいない
5階では新たに1人が利用
結局利用した人数が最も少ないときは,$1+6+1=8$(人),最も多いときは,$1+9+1=11$(人)。
答えは 8人以上11人以下
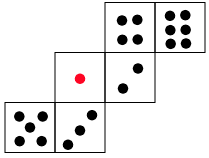
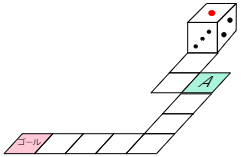
4 図はさいころの展開図です。このさいころを,図のようなすごろくの上をすべることなく転がしていくことを考えます。
次の問いに答えなさい。
10点×2=20(点)
(1) Aの位置に来たとき,さいころの上の面の数字は何ですか。
こたえ
さいころは図のようになります。

最初の2回の移動では次のようになります。
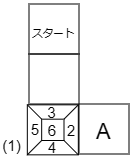
そしてAの位置に移動すると下の図のようになります。
答えは 5
(2) ゴールに着いたとき,さいころの上の面の数字は何ですか。
こたえ
さいころを転がすときの考え方のポイントです。
① 同じ方向に4回転がすのは,転がさないのと同じ。
② ある方向に3回転がすのは,逆向きに1回だけ転がすのと同じ。
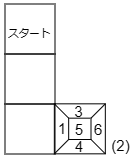
Aを通過したあと下方向に3回転がりますから,上のポイント②により上側に1回に転がすのと同じです。従って下の図のようになります。

そしてゴールへは左に4回転がしますが,ポイント①により,同じ方向に4回転がしたときの目の配置は転がさないときと同じです。
よって答えは 4

