
1 次の計算をしなさい。
10点×4=40(点)
(1) $147-1.96-0.04$
こたえ
前から順番に引き算を行ってもよいのですが,147から引く数の合計に着目してみましょう。1.96 と 0.04 の2つを引くのですから,合計すると 1.96+0.04=2 です。これを147から引くと 147-2=145
答えは 145
(2) $8.3\times1.2+8.3\times8.8$
こたえ
計算の工夫をしてみましょう。結合のきまりを使うと問題の式は\[8.3\times(1.2+8.8)\]となります。1.2+8.8=10 ですから,結局 8.3×10=83
答えは83
(3) $610.45\div145$
こたえ
わり算を行うとき,小数点の位置をまちがわないように気をつけましょう。
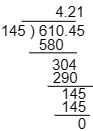
(4) $36\div(7.1-17.6\div8\div2)$
こたえ
カッコの中が先で,その中でもわり算が優先です。わり算が連続して続くときは,前から順に計算していきます。
まず,17.6÷8=2.2 です。次に 2.2÷2=1.1です。よって 7.1-1.1=6 ですから,最後に 36÷6=6
答えは 6
2 あやさん,まゆさん,りおさんの3人がかるたをして遊んでいます。かるたは全部で50枚です。現在あやさんが15枚,まゆさんが9枚,りおさんが12枚です。りおさんが必ず1番になるためには,りおさんはあと何枚とればよいでしょうか。
10点
こたえ
14+9+12=35ですから,残りの枚数は50-35=15(枚)です。「必ず1番」というのは「最悪の状況でも1番」ととらえてください。最大のライバルはあやさんです。最悪の状況とはあやさんがとり続けることです。ですからりおさんとしては,このあとまゆさんは1枚も取らず,あやさんがとり続けた場合を考えて,その場合であっても1番になるために必要な枚数を考えます。
まず,りおさんが3枚とると,あやさんと同じ15枚になります。これで残りは15-3=12(枚)です。りおさんとあやさんが6枚ずつ取ると同点となってしまいますから,りおさんとしては7枚とると残りの5枚をあやさんがとっても1番になれます。もちろんまゆさんが5枚とってもりおさんが1番であることに変わりません。結局りおさんは,3+7=10(枚)とると,必ず1番になります。
答えは 10枚
3 まいさんはあるダンスチームに所属しています。このチームは8月3日土曜日に行われるダンスの大会に向けて練習をしています。練習は毎週土曜日の午後5時から午後6時30分までと、毎週日曜日が午後4時から午後6時までです。今日が6月13日木曜日だとして次の問いに答えなさい。
10点×3=30(点)
(1) ダンスの大会は何日後ですか。
こたえ
6月は30日まで,7月は31日まであります。
6月が残り30-13=17(日)
7月が31日
8月は3日
従って合計は 17+31+3=51(日)
答えは 51日後
(2) ダンスの大会まで練習する日は合計で何日ありますか。
こたえ
今日が6月13日木曜日ですから,まず最初に訪れる土曜日は4日後の6月15日土曜日です。次の日も16日日曜日も練習の日です。1週間は7日ですから6月は
6月15日(土),16日(日)
22日(土),23日(日)
29日(土),30日(日)
の6日間あります。
次に7月です。7月最初の土曜日・日曜日は,7月1日が日曜日ですから
7月 6日(土),7日(日)
13日(土),14日(日)
20日(土),21日(日)
27日(土),28日(日)
の8日間あります。
8月は3日土曜日が本番ですからもう練習はできません。
結局練習する日は 6+8=14(日) あります。
答えは 14日
(3) ダンスの大会まで練習する時間は合計で何時間何分ありますか。
こたえ
(2)を考えている中で,土曜日は6月が3回,7月が4回,合計7回あります。土曜日は1.5時間の練習ですから,7×1.5=10.5(時間)です。
次に日曜日は6月が3回,7月が5回ありますから合計8回あります。日曜日の練習は2時間ですから 8×2=16(時間)です。
よって土曜日と日曜日の練習時間を合わせると\[10.5+16=26.5\]となります。0.5時間は30分ですから答えは 24時間30分
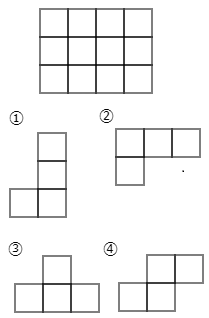
4 (1) 次のようなたて3マス,横4マスの長方形のマス目があります。①~④のピースのうち3つを使って長方形のマスにすき間なくしきつめるとき,使わないピースは①から④のどれですか。ただしピースは回転させてもよいですが,おもてとうらをひっくり返してはいけません。
10点
こたえ
まずは長方形にはマス目が12個あり、①~④のピースはすべてマス目が4個でできていますから,全部足すと4×4=16なので,4枚多くなります。従って,①~④のうち,1枚だけが不要なピースです。
この問題はパズルゲームとして考えても面白いですが、実はパズルが完成させなくても答えがわかるすごい方法があります。
それはマスに色を塗っていく方法です。このときお隣りのマスと色が同じにならないようにします。マス目に色を塗り分ける方法は次の(あ)と(い)の2通りがありますが,いずれの場合も色を塗ったマス目は半分の6枚です。
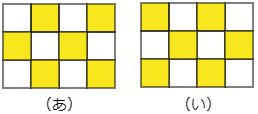
次に同じようにして各ピースにも色を塗っていきます。すると①と②と④は色を塗られるマスが2枚ですが,③だけは塗り場所によって次の(う)と(え)の2パターンあって,(う)だと1枚,(え)だと3枚になります。
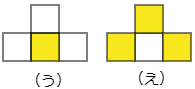
色を塗らなければいけないのは6枚でした。①,②,④を使うときは色を塗るマス目が2枚ずつ増えて2+2+2=6となりますが,③を使うとなると1を足すか3を足すかとなって合計が6になりません。従って使用しないピースは③です。
答えは ③
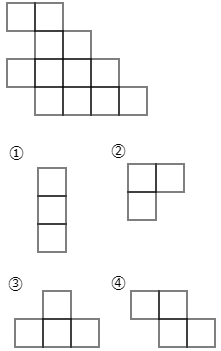
(2) 次のようなマス目に,下の①から④のうちのピースのうち1つだけを複数使ってすき間なくしきつめるとします。どのピースだけを用いればよいですか。ただしピースは回転させてもよいですが,おもてとうらをひっくり返してはいけません。
10点
こたえ
まず,必要なピースの個数ですが,元の図形には12枚のマス目がありますから,①のピースだけを使う場合は4個使います。同じように考えて②のピースだけだと4個,③のピースだけだと3個,④のピースだけだと3個使います。
①のピースだけではしきつめることができないことは,いくつか当てはめてみるとわかります。同じようにして,②のピースだけでもしきつめることはできません。
あとは③か④です。これもパズルゲームとして考えても面白いですが,(1)と同じように色分けしていきましょう。元のマス目は次の(お)と(か)の2通りが考えられますが、いずれの場合も色を塗るのは6枚です。
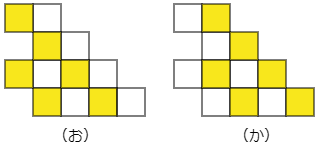
ピースの方も同じように塗り分けて見ましょう。
(1)でみたように,③のピースに色が塗られるマス目は1個か3個のいずれかです。かりに③のピースだけを3個使ってしきつめようとすると,1か3のいずれかを3つ足して合計6にしなければなりませんが,それはできません。
④のピースはどのように塗っても2枚に塗られますから,2×3=6で確かに色が塗られたマス目が6枚になります。実際,次のようにしきつめることができます。
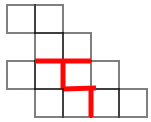
答えは ④

