
1 次の計算をしなさい。
10点×4=40(点)
(1) $10-1\dfrac13-3\dfrac23$
こたえ
前から順番に引き算を行ってもよいのですが,10から引く数の合計に着目してみましょう。$1\dfrac13$ と $3\dfrac23$ の2つを引くのですから,合計すると $1+3=4$ で,$\dfrac13+\dfrac23=\dfrac33=1$ ですから $4+1=5$ だけひくことになります。よって 10-5=5。
答えは 5
(2) $8.3\times2.569-8.3\times0.569$
こたえ
計算の工夫をしてみましょう。8.3が2つ出てきていますから,結合の決まりを使って\[8.3\times(2.569-0.569)\]となります。$2.569-0.569=2$ ですから,結局\[8.3\times2=16.6\] 答えは 16.6
(3) $100-0.015$
こたえ
小数点の位置に気を付けましょう。

(4) 4.11L+1.5dL-0.05Lは何Lですか。
こたえ
1.5dLをLになおすと0.15Lですから\[4.11+0.15-0.05=4.21\] 答えは 4.21L
2 赤,青,黄,白の玉が20個ずつ入った箱があります。この中から何個か玉を取り出すとき,いずれかの色の玉を確実に5個以上取り出すためには,少なくとも何個取り出せばいいですか。
10点
こたえ
最悪のケースを考えてみると,それは赤も青も黄も白も4個ずつ,合計16個も取り出したのにまだ1色も5個以上ない場合です。しかしもう1個取り出すと4つの色のうちどれか1色は5個となります。
答えは 17個
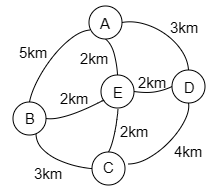
3 ある地域にはA町からE町の5つがあり,図のようにそれぞれの町が道でつながっています。道の長さは図に書かれている通りです。
次の問いに答えなさい。

10点×3=30(点)
(1) A町から出発して,すべても町を少なくとも1度は訪れたのち,ふたたびA町に帰ってくる方法のうち,道のりが最も短いものの長さを求めなさい。ただし,一度通った道は再び通らないとします。
こたえ
例えば,A→B→C→E→D→Aとたどると,\[5+3+2+2+3=15\] 答えは 15km
(2) E町から出発して,すべても町を少なくとも1度は訪れたのち,ふたたびE町に帰ってくる方法のうち,道のりが最も短いものの長さを求めなさい。ただし,一度通った道は再び通らないとします。
こたえ
例えば,E→C→B→A→D→Eとたどると,\[2+3+5+3+2=15\] 答えは 15km
(3) 新たにB町とE町をつなぐ2kmの道路が完成しました。A町から出発して,すべても町を少なくとも1度は訪れたのち,ふたたびA町に帰ってくる方法のうち,道のりが最も短いものの長さを求めなさい。ただし,同じ道を通ってもかまいません。
こたえ
例えば,A→E→B→C→D→Aとたどると,\[2+2+3+4+3=14\] 答えは 14km
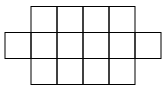
4 (1) 次の図はいくつかの正方形でできています。図の中に正方形はいくつありますか。
10点
こたえ
正方形1個分のもの:14個
正方形4個分のもの:6個
正方形9個分のもの:2個
合計 14+6+2=22
答え 22個
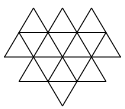
(2) 次の図はいくつかの正三角形でできています。図の中に正三角形はいくつありますか。
10点
こたえ
正三角形1個分のもの:16個
正方形4個分のもの:8個(逆さま3個を含む)
正方形9個分のもの:2個(逆さま1個を含む)
合計 14+8+2=24
答え 24個

