
1 次の計算をしなさい。
10点×4=40(点)
(1) $5\dfrac27-1\dfrac47+\dfrac97$
こたえ
$\dfrac27$ から $\dfrac47$ は引けませんから,5を4と1に分けて,1を $\dfrac77$ として引き算しましょう。\[5\dfrac27=4+\frac77+\frac27=4\frac97\] よって\[4\frac97-1\frac47=3\frac57\] 従って\[3\frac57+\frac97=3\frac{14}7=3+2=5\]
答えは 5
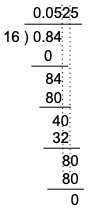
(2) $0.84\div16$
こたえ
小数点の位置に気をつけましょう。
(3) $5.14\times17-3.14\times17$
こたえ
分配の決まりを使います。
$5.14\times17-3.14\times17=(5.14-3.14)\times17=2\times17$
よって答えは 34
(4) 10.2dL+5.3L-1000mLは何Lですか。
こたえ
まずは全て単位をL(リットル)にしましょう。
d(デシ)は10分の1を意味します。従って1dLは1Lの10分の1です。よって,10.2dLは1.02L。m(ミリ)は1000分の1を意味しますから,1mLは1Lの1000分の1です。よって,1000mLは1Lです。
従って 1.02+5.3=6.32。そして, 6.32-1=5.32
答えは 5.32 L
2 $2\times2\times2\times\cdots\times2$ のように2を22回かけたとき,一の位の数字は何ですか。
10点
こたえ
実際に2を22回かけるのは大変です。実はそのようなことをしなくても,一の位だけ見ていけば良いのです。
1回かける 2
2回かける 2×2=4
3回かける 2×2×2=8
4回かける 2×2×2×2=16
5回かける 2×2×2×2×2=32
6回かける 2×2×2×2×2×2=64
一の位だけを見ると[2,4,8,6,2,4,\cdots]となっています。何か気がつきましたか?そうです,「2, 4, 8, 6」の4つの数字のくり返しです。2を22回かけるのですから,「2, 4, 8, 6」の4つの数字が何回くり返されるかというと,22÷4=5あまり2です。よって,「2, 4, 8, 6」の2つ目の数字が求める数字です。
答えは 4
3 りおさんとあやさんは,日本とアメリカのお金について話しています。
りお「日本のお金とアメリカのお金ってと違うらしいわ。」
あや「そうなの。日本のお金の単位は円だけど,アメリカはドルっていうのよ。」
りお「日本の1円とアメリカの1ドルは同じ金額なの?」
あや「違うわ。今は1ドルが160円くらいと同じ金額なの。アメリカの1ドルが日本円のいくらになるかは日々変化しているのよ。」
りお「円高とか円安という言葉をニュースで聞いたことがあるわ。」
あや「アメリカのものを買うときは,日本円をアメリカドルに交換してから買い物をするでしょう?アメリカのある物を買おうとするとき,より安くお買い物ができるような方向に円とドルの交換条件が変化することを「円高」というのよ。これは「円の価値が高くなった」という意味ね。そしてその逆が「円安」よ。」
この会話を元にして,次の問いに答えなさい。
10点×3=30(点)
(1) ある日1ドルが160円でした。翌日1ドルが158円になりました。円高になりましたか,それとも円安になりましたか。
こたえ
例えば1ドルで売っていたお菓子が,160円から158円で買えるようになったということです。つまり今までよりはらうお金が少なくてすむのです。モノが安く買えるようになったのですから,日本円の価値が上がったわけです。
答えは 円高
(2) 1ドルが160円とします。アメリカで売っている15ドルの商品は,日本円でいくらですか。
こたえ
160×15=2400
答えは 2400円
(3) 1ドルが160円とします。日本で売っている2240円の商品は,アメリカドルでいくらですか。
こたえ
(2)とは逆に考えます。160円が1ドルですから,例えば320円は320÷160=2で2ドルです。480円は480÷160=3で3ドルです。このように考えると 2240÷160=14
答えは 14ドル
4 次の角度を求めなさい。
10点×2=20(点)
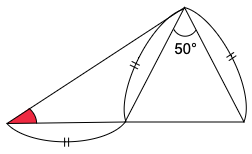
(1) 赤色の角は何度ですか。
こたえ
50°の角をもつ三角形ADCはAD=ACの二等辺三角形ですから,残りの2つの角の大きさは等しくなります。そして三角形ABDもDA=DBの二等辺三角形ですから、求める角の大きさは次の図のようになります。
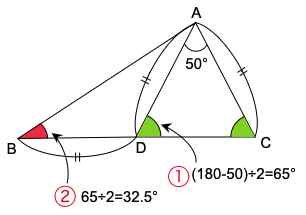
答えは 32.5°
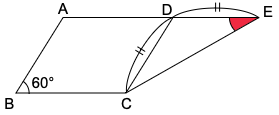
(2) 四角形ABCDは平行四辺形で,三角形CDEはDC=DEの二等辺三角形です。赤色の角は何度ですか。
10点
こたえ
平行四辺形は,お向かいの角の大きさが等しいという性質があります。
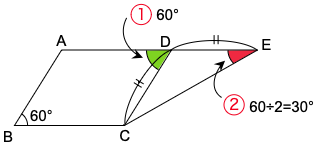
答えは 30°

