
1 次の計算をしなさい。
10点×4=40(点)
(1) 245+345+445
こたえ
すべてたし算ですから,整数の部分と分数の部分に分けて計算しましょう。2+3+4=9。そして45+45+45=125=225 よって,9+225=1125 答えは 1125_
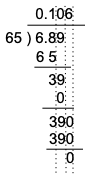
(2) 6.89÷65
こたえ
小数点の位置に気をつけましょう。
(3) 1234×99 (計算を工夫して求めなさい。)
こたえ
計算の工夫をしてみましょう。分配の決まりを使うと計算がとてもラクになります。99=100-1 ですから,1234×99=1234×(100−1)=1234×100−1234×1=123400−1234=122166 答えは 122166
(4) たて0.2m,横500mm,高さ1mの直方体の体積は何cm3ですか。
こたえ
求める単位がcm3ですから,辺の長さをすべてcmになおしてから計算しましょう。
単位の換算(かんさん)
1 m = 100 cm =1000 mm
0.2mは20cm,500mmは50cm,1mは100cm。よって
20×50×100=100000
答えは 100000cm3_
2 「4▼2▲1△」を「とけい」,「3○2▽9○」を「さくら」と読む暗号があります。では「4○1▼9▽」は何と読みますか。
10点
こたえ
ひさしぶりにおしりたんてい問題です。この暗号をぷぷっと解決していきましょう。
まず「4▼2▲1△」ですが,これが「とけい」ですから「4▼|2▲|1△」と考えて,「4▼」が「と」,「2▲」が「け」,「1△」が「い」とします。
「と」はた行,「け」はか行,「い」はあ行ですから,数字が「あかさたな…」であると考えられます。
また「と」はた行の5番目,「け」はか行の4番目,「い」はあ行の2番目ですから,「▼」が5番目を表す記号,「▲」が4番目を表す記号,「△」が2番目を表す記号と考えられます。
| わ | ら | や | ま | は | な | た | さ | か | あ | |
| い | △ | |||||||||
| け | ▲ | |||||||||
| と | ▼ |
次に「3○2▽9○」が「さくら」ですから,次のようになると考えられます。
| わ | ら | や | ま | は | な | た | さ | か | あ | |
| ら | さ | ○ | ||||||||
| い | △ | |||||||||
| く | ▽ | |||||||||
| け | ▲ | |||||||||
| と | ▼ |
従って「4○1▼9▽」の位置は次のようになります。
| わ | ら | や | ま | は | な | た | さ | か | あ | |
| ら | た | さ | ○ | |||||||
| い | △ | |||||||||
| る | く | ▽ | ||||||||
| け | ▲ | |||||||||
| と | お | ▼ |
答えは タオル
3 まゆさんとりくさんは,電気代について話しています。
まゆ「きのう6月の電気代の請求書がきてて,お母さんがとても高くなったって言っていたわ。」
りく「うちも同じことを言ってたよ。電気料金が上がっているんだって。」
まゆ「毎月の電気代ってどうやって決まるの?」
りく「毎月の電気の使用量によって決まるんじゃないかな。ちょっと調べてみない?」
まゆ「そうしましょう。」
2人は電気料金の決まり方について調べました。まゆさんの家庭では,電気料金は次のようにして決まっていることがわかりました。
まゆ「うちの場合,まず基本料金が1700円だったわ。」
りく「基本料金って何?」
まゆ「これは電気を使っても使わなくても毎月決まってかかる料金のことらしいわ。」
りく「なるほど。」
まゆ「そしてこの基本料金に加えて,その月に使った分だけ電気料金がかかるんだけど,それは次の表の通りよ。
| 最初の120kWhまで | 35円 |
| 120kWhをこえ280kWhまで | 40円 |
| 280kWhをこえる分 | 45円 |
りく「kWh(キロワットアワー)というのが電気使用量の単位だね。」
まゆ「そうなの。1kWhだけ使うごとに表のような料金がかかるってことね。」
りく「1kWhあたりの料金は,その月にどれだけ使ってきたかによって3段階に分かれているんだね」
まゆ「これでうちの今月の電気料金が計算できそうだね。」
この会話を元にして,次の問いに答えなさい。
10点×3=30(点)
(1) まゆさんの家庭で,その月の電気使用量が120kWhになったとき,この時点での電気料金はいくらになりますか。
こたえ
1kWhあたり35円ですから,120kWhでは 35×120=4200(円)。基本料金が1700円ですから,合わせると 4200+1700=5900(円)
答えは 5900円
(2) (1)での時点からしばらくたつと,同じ月の電気使用量が280kWhに達しました。(1)の時点から電気料金はいくら増えましたか。
こたえ
表より,120kWhから280kWhまでは,1kWhあたり40円です。120kWhから280kWhまでは,280-120=160kWh ですから,この分の料金は 40×160=6400(円)。
答えは 6400円
(3) まゆさんの家庭では,結局その月に300kWhだけ電気を使いました。その月の電気料金はいくらでしたか。
こたえ
表より,280kWhをこえる分については1kWhあたり45円です。280kWhから300kWhまでは 300-280=20(kWh)。よってこの部分の料金は 45×20=900円。
従って,(1)と(2)の料金と合わせて,5900+6400+900=13200(円)
答えは 13200円
4 次の角度を求めなさい。
10点×2=20(点)
(1) 緑色の角は何度ですか。
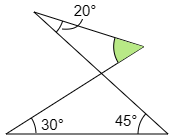
こたえ
三角形の3つの角の合計が180°であることが基本となりますが,三角形の2つの角の合計は,残りの角の外側の角と等しいことを利用するとかんたんです。
下の図で,緑色と水色の角の合計は,赤色の角と等しくなります。
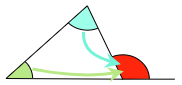
この事実を使っていきましょう。まずはオレンジ色の三角形で上の性質を用いると,黄色の角度が 30°+45°=75° になります。
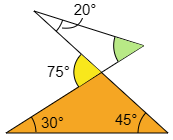
次に水色の三角形に注目すると,20°と緑色の角度を足したものが75°となります。
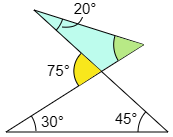
従って求める緑色の角度は 75°-20°=55°
答えは 55°
(2) 緑色の角は何度ですか。
10点
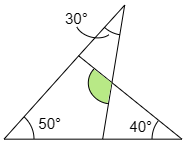
こたえ
(1)と同様に,三角形の2つの角の合計は,残った角の外側と等しいことを使うとかんたんに答えまでたどり着くことができます。
まずオレンジ色の三角形に注目すると,黄色の角度は30°+50°=80°です。
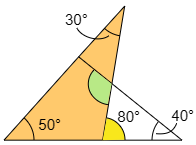
次に水色の三角形に注目すると,40°と黄色の角度を足したものが,求める緑色の角度になります。
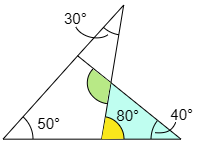
よって見取り色の角度は 40°+80°=120°
答えは 120°

