
1 次の計算をしなさい。
10点×4=40(点)
(1) $123\dfrac2{13}-\dfrac6{13}$
こたえ
123を122と1に分けて,$123\dfrac2{13}$ を
\[122+1+\frac2{13}\]
と見ます。
\[1+\frac2{13}=\frac{13+2}{13}=\frac{15}{13}\]
ですから,こたえは
\[122\frac{15}{13}-\frac6{13}=122\frac{15-6}{13}=\underline{\boldsymbol{122\frac{9}{13}}}\]
(2) $3.56\times 2.3$
こたえ
$356\times23$ を計算すると
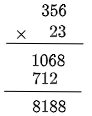
となりますから,小数点を右から$2+1=3$ 番目に打って,こたえは 8.188
(3) $17-\left(4\dfrac25+2\dfrac35-2\times3\right)$
こたえ
まずはカッコ内からですが,たし算・引き算よりかけ算の方が優先ですから,カッコ内は
\[4\dfrac25+2\dfrac35-6\]
となります。$4\dfrac25+2\dfrac35=6\dfrac55=7$ なので,$7-6=1$ です。よってこたえは
\[17-1=\underline{\boldsymbol{16}}\]
(4) 1時間40分30秒+2時間35分54秒=
こたえ
まず秒から足していきましょう。
30秒+54秒は84秒です。ここから60秒を1分としてくり上げます。すると残りは $84-60=24$ 秒です。
次に分を足します。
40分+35分は75分です。秒からくり上がってきた1分を足して76分。ここから60分を1時間としてくり上げます。すると残りは $76-60=16$ 分です。
最後に時間を足します。
1時間+2時間は3時間です。分からくり上がってきた1時間を足して4時間となります。
以上により答えは 4時間16分24秒 です。
2 次の数字はある規則に従って並んでいます。24番目の分数を答えなさい。
10点
こたえ
分子だけを見ていくと
\[1,\ 1,\ 2,\ 1,\ 2,\ 3,\ 1,\ 2,\ 3,\ 4,\ 1,\ \cdots\]
となっています。次に分母だけ見ていくと
\[1,\ 2,\ 1,\ 3,\ 2,\ 1,\ 4,\ 3,\ 2,\ 1,\ 5,\ \cdots\]
となっています。すると問題に与えられたの分数たちは,
\[\frac11\ |\ \frac12,\frac21\ |\ \frac13,\frac22,\frac31\ |\ \frac14,\cdots\]
というようにグループに分けることができます。各グループには分数が
1こ,2こ,3こ,4こ,$\cdots$
というようにふくまれています。分数の個数を数えてみましょう。
1つ目のグループまで 1こ
2つ目のグループまで 1+2=3(こ)
3つ目のグループまで 1+2+3=6(こ)
4つ目のグループまで 1+2+3+4=10(こ)
5つ目のグループまで 1+2+3+4+5=15(こ)
6つ目のグループまで 15+6=21(こ)
7つ目のグループまで 21+7=28(こ)
となっていますから,25番目の分数は7つ目のグループに入っています。7つ目のグループは
\[\frac17,\ \frac26,\ \frac35,\ \frac44,\ \frac53,\ \frac62,\ \frac71\]
とならんでいて,このグループの先頭である $\dfrac17$ は22番目の数ですから24番目の分数はこのグループの3番目,つまり $\underline{\boldsymbol{\dfrac35}}$ です。
3 1辺の長さが3cmの正方形のおり紙Aと,たて3cm,横6cmの長方形のおり紙Bがたくさんあります。
次の問いに答えなさい。
10点×3=30(点)
(1) たて12cm,横15cmの長方形の画用紙があります。この上には折り紙AとBをすきまなく,はみ出すことなく並べます。おり紙を最も多く使う場合と,最も少なく使う場合とでは何枚ちがいますか。
こたえ
最も多く使う場合は折り紙Aだけを使うときです。たてに $12\div3=4$ (枚),横に $15\div3=5$(枚)並べることができますから,使う枚数は
$4\times5=20$(枚)
です。
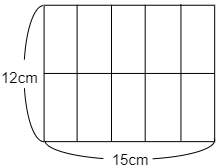
次に最も少なく使う場合は折り紙Bだけを使うときです。例えば図のように並べたとき,たてに $12\div6=2$ (枚),横に $15\div3=5$(枚)並べることができますから,使う枚数は
$2\times5=10$(枚)
です。よって求める枚数は
$20-10=$10(枚)
[別の考え方]
この問題では面積で考えることもできます。画用紙の面積は $12\times15=180({\rm cm^2})$,折り紙Aの面積は $3\times3=9({\rm cm^2})$,折り紙Bの面積は $3\times6=80({\rm cm^2})$ です。
折り紙Aだけ使うときは
$180\div9=20$(個)
折り紙Bだけ使うときは
$180\div18=10$(個)
です。よって求める枚数は
$20-10=\,$10(枚)
(2) たて9cm,横15cmの長方形の画用紙があります。この上には折り紙AとBをすきまなく,はみ出すことなく並べます。おり紙を最も多く使う場合と,最も少なく使う場合とでは何枚ちがいますか。
こたえ
最も多く使う場合は折り紙Aだけを使うときです。たてに $9\div3=3$ (枚),横に $15\div3=5$(枚)並べることができますから,使う枚数は
$3\times5=15$(枚)
です。
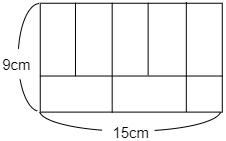
次に最も少なく使う場合は折り紙Bをできるだけ多く使うときです。例えば図のように並べると使う枚数は8枚です。右下の1枚のみ正方形であることに注意してください。
よって求める枚数は
$15-8=\,$7(枚)
(3) おり紙AとBを自由に4枚使って長方形を作ります。何種類の長方形が作れますか。ただし,並べ方が違っていても,同じ形の長方形になるときは,それらを区別せずに1通りとして数えます。また,回転させると同じになるものも区別しません。
こたえ
折り紙Aと折り紙Bの使う枚数の組合せは
| おり紙A | 0 | 1 | 2 | 3 | 4 |
| おり紙B | 4 | 3 | 2 | 1 | 0 |
の5通りです。順番に確認していきましょう。
①折り紙Aが0枚,折り紙Bが4枚のとき
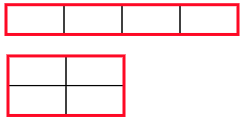
この2通りです。
②折り紙Aが1枚,折り紙Bが3枚のとき

この1通りです。
③折り紙Aが2枚,折り紙Bが2枚のとき
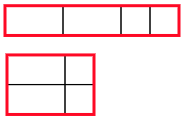
この2通りです。
④折り紙Aが3枚,折り紙Bが1枚のとき
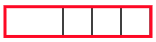
この1通りです。
⑤折り紙Aが4枚,折り紙Bが0枚のとき
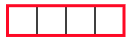
この1通りです。
以上により,求めるものは
$2+1+2+1+1=\,$7種類
4 図のようなさいころがあります。このさいころは向かい合う面の目の数を足すと常に7になります。
次の問いに答えなさい。
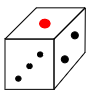
10点×2=20(点)
(1) 次の図は上のさいころの展開図です。残った面の目の数を書きなさい。ただし,「4,5,6」といったように数字で書きなさい。
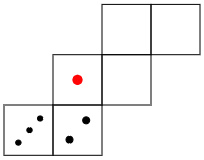
こたえ
ヒントのように展開図の一部を移動させて考えましょう。
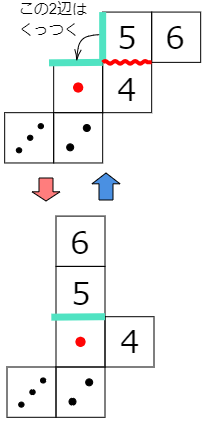
答えは図のようになります。
ポイント
立方体の展開図では,角度が90°になっている辺どうしは,組み立てたとき必ず重なります。
(2) さいころが図のようにおいてあります。前に5回転がしたあと,右に7回転がすとき,上の面にきている目の数は何ですか。「1,2,3,4,5,6」の数字で答えなさい。ただし,$90^\circ$ 回転させるごとに1回と数えることにします。
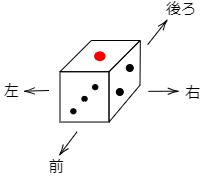
こたえ
さいころを転がす問題のポイントは
ポイント
- 同じ方向に4回転がすのは,転がさないのと同じ
- ある方向に3回転がすのは,それとは反対の方向に1回だけ転がすのと同じ
の2点です。
さて,さいころを実際に転がす前に,問題にあるさいころをかいておきましょう。ただし,立体的に書くのはむずかしい上に,いくつかの面の数が書きにくいですよね。そこで,さいころを真上から見た次のような図をかくことにします。
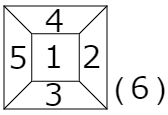
とてもさいころが見やすくなりましたね。しかしこの図でも,真下の面の数だけは書くことができませんので,カッコ書きで「(6)」というように書いておきましょう。
このさいころをまずは前に5回転がしていきます。ポイント①で見たように,前に $5-4=1$ 回だけ転がすのと同じです。よってさいころは次の図のようになります。
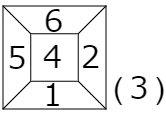
次に右に7回転がします。4回転がすと転がさないのと同じでしたから,$7-4=3$ 回だけ転がします。ここでポイント②です。右に3回転がすのはそれと反対方向の左に1回だけ転がすのと同じです。ですからさいころは次の図のようになります。
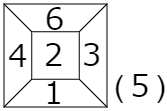
従って,求める数字は 2 です。

