１ 次の計算をしなさい。
10点×4=40(点)
(1) $5\dfrac67+\dfrac{17}7$（帯分数で答えなさい。)
こたえ
分数どうしを足して，仮分数から帯分数になおします。
$\dfrac67+\dfrac{17}7=\dfrac{6+17}7=\dfrac{23}7$
$23\div7=3$ あまり2
よって $\dfrac{23}7=3\dfrac27$
したがってこの3と $5\dfrac67$ の5を足して8
答えは $8\dfrac27$
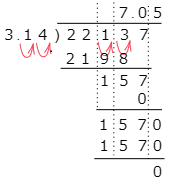
(2) $22.137\div3.14$
こたえ
小数点の位置に気をつけましょう。
(3) $450.1\times0.57-450.1\times0.56$ (計算を工夫して求めなさい。)
こたえ
計算の工夫をしてみましょう。分配の決まりを使うと計算がとてもラクになります。
$450.1\times0.57-450.1\times0.56=450.1\times(0.57-0.56)$
0.57-0.56=0.01 ですから
450.1×0.01＝4.501
答えは 4.501
(4) たて10cm，横50cm，高さ120cmの直方体の体積は何L(リットル)ですか。
こたえ
この直方体の体積は 10×50×120＝60000(cm3)
1Lは1辺の長さが10cmの立方体の体積ですから，10×10×10＝1000(cm3)です。
よって60000(cm3)の0を3こ消します。
答えは 60L
２ 1から4までが書かれた4枚のカードが2組あります。まず1組目を図のように1から4と順番に並べます。
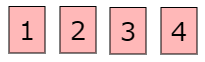
そしてもう1組をそのすぐ下に並べるのですが，このときすぐ上のカードと同じ数字にならないように並べる方法は何通りありますか。
10点
こたえ
「もれなく，ダブりなく」数えましょう。この問題はちょっと難しい問題なので，じっくり落ち着いて考えてください。
すべて書きつくすと次のようになります。
元のならび方 １２３４
ーーーーーーーーーーーーーーーーー
ならべかえたあと ２１４３
２３４１
２４１３
３１４２
３４１２
３４２１
４１２３
４３１２
４３２１
答えは 9通り
３ 次の，ふうかさんとかなえさんの会話を読んで，あとの問いに答えなさい。
ふうか「この前遊園地に行ったのよ。とても楽しかったわ。」
かなえ「へえ、いいわね。どんな乗り物に乗ったの？」
ふうか「コーヒーカップとか、ゴーカートとかいろいろ乗ったわ。料金も安いのよ。」
ふうかさんは料金を紙に書きました。
メリーゴーランド 100円
ゴーカート 100円
観覧車 200円
大回転ブランコ 200円
コーヒーカップ 200円
きかん車 300円
かなえ「本当！これならおこづかいでも乗れそうだわ。」
ふうか「私はゴーカート2回と，大回転ブランコ2回，コーヒーカップ1回乗ったわ。」
かなえ「じゃあ，料金は全部で（ ア ）円ね。
ふうか「うん，そうね。私は入園するときに1000円で1200円分遊べるチケットを買ったの。」
かなえ「それって（ イ ）割分お得ってことね。」
ふうか「そう。だから残りのチケットを使ってお母さんと2人で（ ウ ）に1回だけ乗って，チケットを使い切ったわ。」
10点×3=30(点)
(1) （ ア ）に入る数字を求めなさい。
こたえ
ゴーカート3回で 100×3＝300(円)
大回転ブランコ2回で 200×2＝400(円)
コーヒーカップ1回で 200円
合計 300＋400＋200＝800(円)
答えは 800円
(2) （ イ ）に入る数字を求めなさい。
こたえ
「1割」というのは全体の10分の1のことを言います。1000円の1割分は100円です。
200円分だけ得をしたのですから，2割です。
答えは 2
(3) （ ウ ）に入るものをふうかさんのメモの中から選びなさい。ただし，会話文の中でふうかさんが乗った述べたものには乗らなかったとします。
こたえ
チケットをちょうど使い切ったという部分に注意しましょう。
（ ア ）が900円ですからチケットの残りは1200－900＝300(円)です。この300円をちょうど使い切る乗り物はきかん車です。
答えは きかん車
４ 次の図は点Oを中心とする円の中に三角形があります。以下の問いに答えなさい。
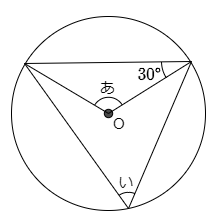
10点×2=20(点)
(1) 角度「あ」の大きさを求めなさい。
こたえ
円というのは，中心から円周上までの長さがどこも等しい図形です。すると図の水色の三角形が二等辺三角形です。
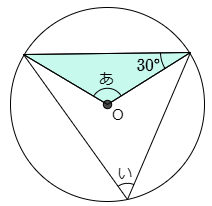
すると「あ」ではない残りの角も30°ですから，30°＋30°＝60°
よって 180°ー60°＝120°
答えは 120°
(2) 角度「い」の大きさを求めなさい。
こたえ
まずむらさき色の線を引きます。すると図で示した赤い2つの○と，水色の2つの□はそれぞれ角の大きさが同じですから，これまで何度もやってきた三角形の角度の関係を用いると○2個分と，□2個分の合計が角度「あ」であることがわかります．
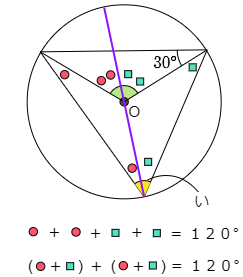
「い」は赤色の○印と水色の□をそれぞれ1こずつ足したものですから60°です。
答えは 60°
