１ 次の計算をしなさい。
10点×4=40(点)
(1) $16\dfrac4{13}-1\dfrac7{13}$（帯分数で答えなさい。)
こたえ
$\dfrac4{13}$ から $\dfrac7{13}$ は引きませんから，16から1だけ $\dfrac{13}{13}$ にし $\dfrac{13}{13}+\dfrac4{13}=\dfrac{17}{13}$ とします。
分数の計算は $\dfrac{17}{13}-\dfrac7{13}=\dfrac{10}{13}$
整数の計算は 15-1=14
よって答えは $14\dfrac{10}{13}$
(2) 16＋128÷16÷4＋2×(13-3×4)
こたえ
たし算ひき算よりかけ算，わり算の方を先にやります。カッコがある場合はさらにカッコ内の計算を先にやります。また，わり算が連続している場合は，前から順番に計算しなければなりません。
128÷16＝8， 8÷4＝2
また，
3×4＝12， 13－12＝1， 2×1＝2
従って
16＋2＋2＝20
答えは 20
(3) 1.15×1123＋0.85×1123
こたえ
計算の工夫をしてみましょう。分配の決まりを使うと計算がとてもラクになります。
1.15×1123＋0.85×1123＝(1.15＋0.85)×1123
カッコ内を計算すると 1.15＋0.85＝2
よって 2×1123＝2246
答えは 2246
(4) 10L(リットル)入る容器に45dL(デシリットル)だけ水を入れました。あと何cm3水を入れることができますか。
こたえ
1Lは1辺の長さが10cmの立方体の体積です。つまり$10\times10\times10=1000({\rm cm}^3)$ が 1L です。
45dLは4.5Lです。
よって残りは 10－4.5＝5.5（L)
１Lは1000cm3ですから
5.5×1000＝5500（cm3）
答えは 5500 cm3
２ ある町には2つの学校があります。各学校の児童の数は百の位までの概数でそれぞれ500人，700人です。2つの学校の児童の数を合わせた数として考えられるのは何人以上，何人以下ですか。
10点
こたえ
百の位までの概数ということは十の位の数を四捨五入したということです。
百の位までの概数で500人ということは
450人以上，549人以下
です。
百の位までの概数で700人ということは
650人以上，749人以下
です。
よって合計の人数は最も少ないときで
450＋650＝1100(人)
最も多いときで
549+749=1298(人)
答えは 1100人以上，1298人以下
３ 60L(リットル)入る容器に水を入れるために2つの蛇口AとBがあり，それぞれ一定の割合で水を入れることができます。最初は蛇口Aだけを使って水を入れ，途中から蛇口Bだけを使って水を入れたところ，水を入れ始めてからの時間と，入った水の量の関係は次のグラフのようになりました。
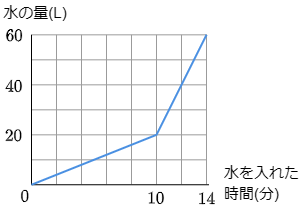
次の各問いに答えなさい。
10点×3=30(点)
(1) 蛇口Aは1分間に何Lの水を入れることができますか。
こたえ
グラフを見ると，蛇口Aを使ったのは，グラフが折れ曲がる手前のと10分間で，その間に水が20L入っています。よって
20÷10＝2(L)
答えは 毎分2L
(2) 蛇口Bは1分間に何Lの水を入れることができますか。
こたえ
蛇口Bを使ったのは，グラフが折れ曲がっている10分後からで，14分後までの4分間です。その間に60－20＝40(L)の水が入ったので
40÷4＝10(L)
答えは 毎分10L
(3) 容器に水がない状態から2つの蛇口を両方とも使って水を入れると，何分で満水になりますか。
こたえ
(1)と(2)で求めた値を利用します。2つの蛇口を両方とも使うと1分間に2＋10＝12(L)の水を入れることができますから，
60÷12＝5(分)
答えは 5分
４ 次のさいころは向かい合う面の数を足すと７になります。
次の各問いに答えなさい。
10点×2=20(点)
(1) このさいころの展開図を完成させなさい。さいころの目は「４，５，６」のように数字で書きなさい。
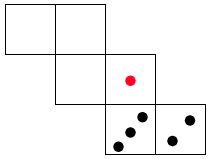
こたえ
展開図における法則を覚えていますか？
①角が最も小さい2辺は組み立てたとき重なる。
②重なる2辺のとなりどうしも重なる
でした。
答えは図のようになります。
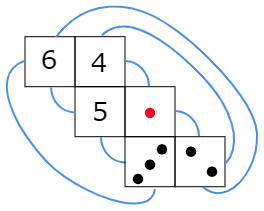
(2) このさいころを，接している(くっついている)面の数が同じになるように並べました。図の「あ」の面にある数を答えなさい。
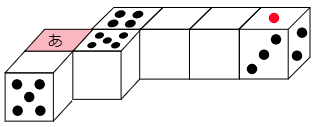
こたえ
さいころを真上から見た図は次のようになります。
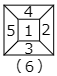
図のようにさいころをかいて，必要なところだけ順に数字をうめていきます。
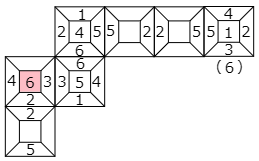
答えは 6
