１ 次の計算をしなさい。
10点×4=40(点)
(1) $\dfrac{21}4-1\dfrac34$ (帯分数で)
こたえ
$\dfrac{21}4$ を帯分数にして考えてもよいし，$1\dfrac34$ を仮分数にしてから考えてもよいし，どちらでもよいでしょう。どちらかと言えば，$1\dfrac34$ を仮分数にしてから考えるほうが，ラクにできると思います。
$1\dfrac34=\dfrac{4+3}4=\dfrac74$
よって
$\dfrac{21}4-\dfrac74=\dfrac{21-7}4=\dfrac{14}4=3\dfrac24$
答えは $\underline{\boldsymbol{3\dfrac24}}$
(2) 6.2×3.7
こたえ
小数点の位置に気を付けましょう。
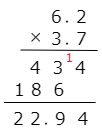
(3) 36と54の最小公倍数と最大公約数を求めなさい。
こたえ
公倍数の求め方は，36の倍数をいくつか書き，54の倍数もいくつか書き，最初に同じ数字が出てきたものが最小公倍数です。
36の倍数：36, 72, 108, 144, …
54の倍数：54, 108, …
最小公倍数は １０８
最大公約数の方は，36の約数をすべて書き，54の約数もすべて書き，共通する約数に印をつけていきます。そしてその中で最大の数が最大公約数です。
36の約数：1, 2, 3, 4, 6, 9, 12, 18, 36
54の約数：1, 2, 3, 6, 9, 18, 27, 54
最大公約数は １８
(4) 2.5L(リットル)入る容器に，1回で400㏄ 計ることのできるカップで4回水を入れ，残りを150cm3 計ることのできるカップで水を入れると何回で容器が満水になりますか。
こたえ
1Lは1000ccです。また，1辺が10cmの立方体の体積が1Lです。
まず400㏄で4回入れたので 400×4=1600(㏄)
これは1.6Lです。
よって残りは 2.5－1.6=0.9(L)
これは900cm3です。
従って150cm3のカップで水を入れると
900÷150＝6
答えは 6回
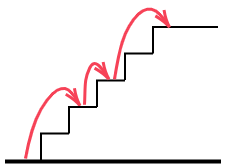
２ 5段の階段をちょうど3回で登りきる方法は何通りありますか。ただし，毎回少なくとも1段は登るとします。下の図は登り方の1つの例で，1回目に2段，2回目に1段，3回目に2段上って5段目に達しています。
10点
こたえ
基準を設定して考えるようにします。1回目に登る段数が
1段のとき …
2段のとき …
3段のとき …
というようにして，1回目の段数を小さい方から増やして考えましょう。
１回目 ２回目 3回目
１ １ ３
１ ２ ２
１ ３ １
２ １ ２
２ ２ １
３ １ １
よって答えは 6通りです。
さて，気が付きましたか？この6通りは前回第24回の問題２
あ ＋ い ＋ う ＝ ５
となる（あ，い，う）の組合せを求めた問題と中身は同じなのです。
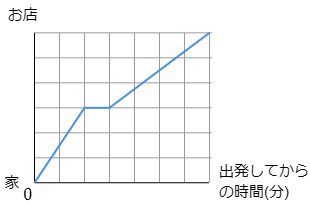
３ らんさんは文房具を買いに，家から1200mはなれたお店に歩いて買いに行きました。途中少し疲れたので4分間休み，そのあと最初よりゆっくりとした速さで歩いてお店まで行きました。下の図はらんさんの移動の様子をグラフに表したものです。
次の各問いに答えなさい。
10点×3=30(点)
(1) らんさんが休んだのは，家を出てから何mのところですか。グラフから判断して答えなさい。
こたえ
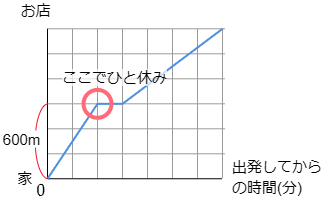
家からお店まで1200mで，それが6めもり分です。従って１めもりは
1200÷6＝200(m)
休んだのは３めもりの所ですから
200×3＝600(m)
答えは ６００ｍ
(2) らんさんは家を出てから休むまで，1分間に何mの速さで歩きましたか。
こたえ
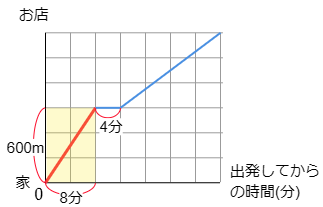
休んだ時間が4分間なので，横の1めもりが4分であるとわかります。
よって，らんさんがひと休みするまで２めもり分ですから
4×2＝8(分)
(1)でそこまでのきょりが600mでしたから1分間に歩き速さは
600÷8＝75(m)
答えは 1分間に75m
(3) らんさんは休んだあと，1分間に何mの速さで歩きましたか。
こたえ
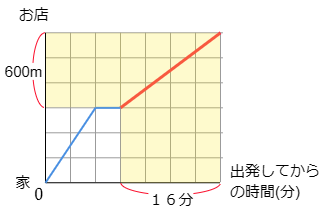
ふたたび歩き始めてからお店までの距離は 1200－600＝600(m)
時間は４めもり分ですから 4×4＝16(分)
よって 600÷16＝37.5(m)
答えは 1分間に37.5m
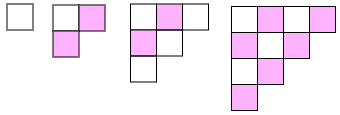
４ 次のように白い正方形1枚から始めて，むらさき色の正方形と交互に並べながら三角形の形を大きくしていきます。次の問いに答えなさい。
10点×2=20(点)
(1) 一番上に並べる正方形の枚数が10枚になったとき，むらさき色の正方形は何枚使いましたか。
こたえ
むらさき色の正方形は，2枚，4枚，6枚，…と増えていきます。横に並べる正方形の枚数が10枚のとき，むらさき色の正方形を並べるのは5回目になりますから，
2＋4＋6＋8＋10＝30(枚)
答えは 30枚
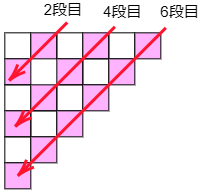
(2) 白色の正方形の使う枚数が，むらさき色の正方形より5枚多くなるのは，一番上に並べる正方形が何枚のときですか。
こたえ
白色の正方形は，1枚，3枚，5枚，…と増えていきますから，合計すると，1枚，1+3=4枚，1+3+5=9枚，…という具合に増えていきます。表にして考えると
| 段数 | 1段目 | 3段目 | 5段目 | 7段目 | 9段目 |
| 白の枚数 | 1 | 3 | 5 | 7 | 9 |
| 合計 | 1 | 4 | 9 | 16 | 25 |
一方，むらさき色の正方形は，2枚，4枚，6枚，…と増えていきますから，合計すると，2枚，2+4=6枚，2+4+6=12枚，…という具合に増えていきます。
| 段数 | 2段目 | 4段目 | 6段目 | 8段目 | 10段目 |
| むらさきの枚数 | 1 | 3 | 5 | 7 | 9 |
| 合計 | 2 | 6 | 12 | 20 | 30 |
表から白色の正方形を9段目に9枚並べると合計25枚になり，8段目までに並べてあるむらさき色の正方形より5枚だけ多くなります。
答えは 9枚
