
1 次の計算をしなさい。
10点×4=40(点)
(1) 12+13−19
こたえ
前から計算してもよいですが,後ろの 13−19 から計算した方がラクかもしれませんね。
13−19=39−19=29.
よって,
12+29=918−418=518
答えは 518
(2) 3.503÷0.5
こたえ
小数点の位置に気を付けましょう。
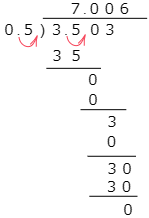
(3) 4m21cm+0.0717kmは何mmですか。
こたえ
4m21cmは4.21m
0.0717km=71.7m
よって 4.21+71.7=75.91m
答えは 75910mm
(4) 6時間2分8秒ー3時間10分50秒は,何時間 何分 何秒ですか。
こたえ
8秒から50秒は引けませんから2分から1分借りてきて,
1分8秒ー50秒=18秒
次に残った1分から10分は引けませんから,6時間から1時間借りてきて
1時間1分ー10分=51分
最後に5時間ー3時間=2時間
答えは 2時間51分18秒
2 ある町の人口は千の位までの概数(がいすう)で,2000年は40000人,2024年は45000人でした。人口は最大で何人増えましたか。
10点
こたえ
千の位までの概数ですから,百の位を四捨五入したのです。2024年で考えられる最も多い人口から,2000年で考えられる最も少ない人口を引けばいいですね。
2000年が千の位までの概数で40000人ですから
39500人以上 40500人未満(つまり40499人以下)
2024年が千の位までの概数で45000人ですから
49500人以上 45500人未満(つまり45499人以下)
よって 45499-39500=5999(人)
答えは 5999人
3 次のように,□が3つと白,赤,青の3色で数字を表すことを考えます。
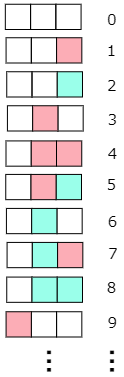
次の各問いに答えなさい。
10点×3=30(点)
(1) 表せる数字の中で,最も大きな数字は何ですか。
こたえ
白を0,赤を1,青を2として書き換えてみましょう。
私たちがふだん使っている数は10を1つのかたまりとして考える数字で,
1の位,10の位,100(10×10)の位,1000(10×10×10)の位
となっています。例えば4217という数字は
10×10×10が4個
10×10が2個
10が1個
1が7個
という風に考えて
4000+200+10+7
と表せます。一方,この問題の数字は3を1つのかたまりとして考えますから
1の位,3の位,9(3×3)の位
となっています。
000 0
001 1
002 2
010 3
011 4
012 5
020 6
021 7
022 8
100 9
⋮ ⋮
このように使える数字は0,1,2の3つです。一番大きい数字は222ですから,
9×2+3×2+1×2=18+6+2=26
答えは 26
※この数字は□を4つ使ってできる数字の一番左の位の数である3×3×3=27の位でる27より1だけ小さい数字です。
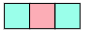
(2) 23を表す図をかきなさい。
こたえ
23は9×2+3×1+1×2(=18+3+2)と表せます。
答えは
(3) 次の計算結果を数字で答えなさい。
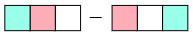
こたえ
それぞれの記号が表す数字が何かを求めて引き算しましょう。
最初の記号が210ですから
9×2+3×1=18+3=21
次の記号が102ですから
9×1+1×2=11
21-11=10
答えは 10
4 次のように正三角形1つから始めて次のような操作(そうさ)を繰り返し行います。
(操作)各辺の長さの 13 の長さの正三角形を作り,各辺のちょうど真ん中にくっつける。そして,くっつけた部分の辺は取りのぞく。
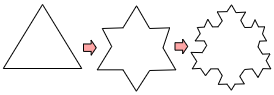
上の図はこの操作を2回行ったときの様子です。
次の各問いに答えなさい。
10点×2=20(点)
(1) この操作を3回行うと,出来上がった図形は何本の折れ線からできていますか。
こたえ
1つの辺に注目してください。この操作を1回行うごとに,1本だった辺が4本の折れ線になっています。つまり4倍です。これがどの辺にも同じように起こっています。
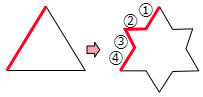
よって
1回目 3×4=12(本)
2回目 12×4=48(本)
3回目 48×4=192(本)
答えは 192本
(2) 最初の正三角形の面積を18cm2とするとき,1回目の操作の後の面積は何cm2ですか。
こたえ
1回目の操作でくっつけた正三角形の面積は元の正三角形の面積の何倍かを図をかいて考えてみましょう。
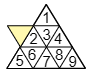
新しくくっつけた黄色の正三角形は元の面積の 19 です。よって黄色の正三角形の面積は
18÷9=2(cm2)
この黄色い正三角形と同じ面積の正三角形が全部で3個くっつきましたから,求める面積は
18+2×3=18+6=24(cm2)
答えは 24cm2

