~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) $500-\dfrac{14}3$
$\dfrac{14}3$を帯分数にしてみます。次に500を $499+1$ と考えて計算を行います。
(2) $24\div(3\times2+24\div6\div2)$
カッコの中を先に計算します。かけ算,たし算,わり算がありますが,優先順位を考えて計算を行いましょう。
(3) $0.106\times45$
まずは小数点がないものとして $106\times45$ を計算します。そして小数点の位置を考えます。
(4) $\rm 2m\,5cm+0.36m$ は何cmですか。
求める単位がcmですから,mをcmに直して考えましょう。
2 ある機械に数字を入力するとその数字を2倍して1をたした数が画面に表示されます。例えば3を入力すると
$3\times2=6$,$6+1=7$
となりますから7が表示されます。花子さんがこの機械にある数字を入力すると画面に39が表示されました。花子さんが入力した数字は何ですか。
10点
□を使って考えてみましょう。
□を2倍して,1を足したら39になったという式を作り,□に当てはまる数字を考えます。
3 1,2,3の数字が書かれたカードが2枚ずつあります。
次の問いに答えなさい。
10点×3=30(点)
(1) 1,2,3の3枚のカードを使って3桁の数字を作ります。数字は何個作れますか。
とりあえず百の位から考えてみましょう。1,2,3の3通りです。図のように書いておきます。
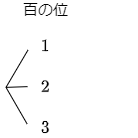
次に十の位です。例えば百の位の数が1のとき,十の位に使えるのは2日3ですから,次のように線をのばして書いておきます。
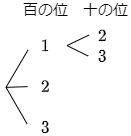
このようにして続きを書いていきましょう。
ちなみにこのような図は、木の枝が広がっていく様子に似ていることから樹形図といいます。
(2) これらのカードから2枚を選んで2桁の数字を作ります。数字は何個作れますか。ただし,同じ数字のカードを使ってもよいとします。
(1)と同じように樹形図を書いて、もれなく、ダブりなく数えましょう。
(3) これらのカードから2枚を選んで2桁の数字を作ります。それらの数字のうち,3で割り切れる数字は何個ありますか。ただし,同じ数字のカードを使ってもよいとします。
3で割り切れる数は多くありませんので、全部調べてみてもよいかもしれませんが、実は3で割り切れる数というのは「各位の数を足すと3の倍数になる」のです!
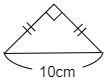
4 図のような直角二等辺三角形があります。
次の問いに答えなさい。
10点×2=20(点)
(1) この三角形の面積を求めなさい。
5年生のこの時期は,まだ三角形の面積を学習していませんが,正方形の面積なら学習していますよね。実はこの三角形を上手に並べると正方形になります。このことからこの三角形の面積が求められるのです。
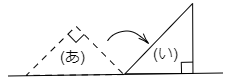
(2) この三角形を図(あ)から図(い)の位置にくるまで回転させました。回転した角度は何度ですか。ただし,三角形の3つの角の合計は180°です。
まず三角形の直角ではない角が何度かを求めます。次に回転する角度ですが,どれか1本の辺に注目し,その辺の動きから回転する角度を求めましょう。