
1 次の計算をしなさい。
10点×4=40(点)
(1) $500-\dfrac{14}3$
こたえ
$\dfrac{14}3$を帯分数にすると, $14\div3=4$あまり2ですから,$4\dfrac23$ となります。よって500を $499+1$ にして
\[500-\frac{14}3=(499+1)-4\frac23\]
とします。$499-4=495$ です。また,$1-\dfrac23$ は1が $\dfrac33$ ですから,
\[1-\frac23=\frac33-\frac23=\frac13\]
となります。よって答えは $\underline{\boldsymbol{495\dfrac13}}$
(2) $24\div(3\times2+24\div6\div2)$
こたえ
カッコの中を先に計算します。掛け算やわり算が先です。
$3\times2=6$ です。$24\div6\div2$ は $24\div6$ を先に計算し,4となります。次にこの4を2で割って2となります。従ってカッコの中は
\[6+2=8\]
です。よって求める答えは
\[24\div8=\underline{\boldsymbol{3}}\]
(3) $1.06\times4.5$
こたえ
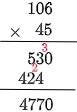
小数点を右から3番目につけて 4.77
(4) $\rm 2m\,5cm+0.36m$ は何cmですか。
こたえ
1mは100cmですから,2m 5cm は 205 cmです。そして0.36mは
$100{\rm cm}\times0.36=36{\rm cm}$
です。よって
$205{\rm cm}+36{\rm cm}=\underline{\boldsymbol{241{\rm cm}}}$
2 ある機械に数字を入力するとその数字を2倍して1をたした数が画面に表示されます。例えば3を入力すると
$3\times2=6$,$6+1=7$
となりますから7が表示されます。花子さんがこの機械にある数字を入力すると画面に39が表示されました。花子さんが入力した数字は何ですか。
10点
こたえ
入力した数字を□とし,逆方向から考えます。
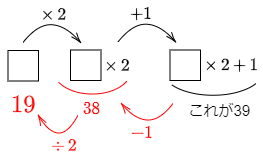
答えは 19
3 1,2,3の数字が書かれたカードが2枚ずつあります。

次の問いに答えなさい。
10点×3=30(点)
(1) 1,2,3の3枚のカードを使って3桁の数字を作ります。数字は何個作れますか。
こたえ
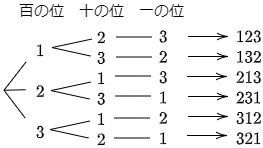
この樹形図から
\[123,132,213,231,312,321\]
の 6個
これを計算で求めることもできます。それは樹形図の枝の数を数えるという方法です。最初の枝(一番左)が3本,そしてどの枝からも2本ずつ枝が出ていますから,ここまで $3\times2=6$(本) の枝があります。最後にこれら6本の枝から1本ずつ出ていますから $6\times1$ で6本あります。この最後の枝(一番右)の数が求めるものとなります。
(2) これらのカードから2枚を選んで2桁の数字を作ります。数字は何個作れますか。ただし,同じ数字のカードを使ってもよいとします。
こたえ
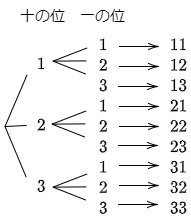
この樹形図から
\[11,12,13,21,22,23,31,32,33\]
の 9個
これを(1)と同じように計算で求めることもできます。最初の枝(一番左)が3本,そのどの枝からも3本ずつ出ていますから,枝の数は $3\times3=9$ 本となっています。ですから求める数字の個数は9個です。
(3) これらのカードから2枚を選んで2桁の数字を作ります。それらの数字のうち,3で割り切れる数字は何個ありますか。ただし,同じ数字のカードを使ってもよいとします。
こたえ
(2)の答えより,9個の数字のうち3で割り切れるのは
\[12,21,33\]
の 3個 です。
実は3で割り切れる数というのはいつも各位の数の合計が3で割り切れる数になっています。上の3つの数は
\[1+2=3,\ 2+1=3,\ 3+3=6\]
となっていて,いずれも3で割り切れます。この考え方を使うと例えば567は
\[5+6+7=18\]
となり,18は3で割り切れますから567も3で割り切れます。実際,$567\div3=189$ です。
4 図のような直角二等辺三角形があります。
次の問いに答えなさい。
10点×2=20(点)
(1) この三角形の面積を求めなさい。
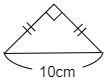
こたえ
この3角形を4枚使って図のように並べると,1辺の長さが10cmの正方形ができます。
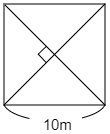
この面積は $10\times10=100|{\rm cm^2}$ です。元の三角形の面積は,この正方形の面積の $\dfrac14$ ですから,求める面積は
\[100\div4=\underline{\boldsymbol{25{\rm cm^2}}}\]
別の考え方
次の図の波線でハサミを入れて,移動させると図のように正方形になります。
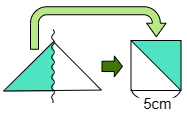
よって求める面積は 5×5=25cm2
(2) この三角形を図(あ)から図(い)の位置にくるまで回転させました。回転した角度は何度ですか。ただし,三角形の3つの角の合計は180°です。
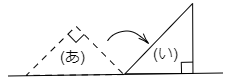
こたえ
三角形の3つの角の合計が180°になることは,5年生の1学期に学習します。この三角形は直角二等辺三角形ですから,直角以外の残り2つの角の大きさは同じになります。
直角以外の残りの角の合計は
\[180-90=90^\circ\]
この角を残りの2つで分け合いますから,残りの角の1つは
\[90\div2=45^\circ\]
です。
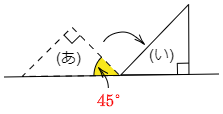
この準備のもとで,回転した角を求めていきましょう。図の赤色の辺に注目してください。

この赤色の辺が青色のところまで来ていますね。
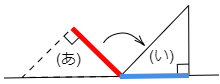
すると求めるものは次の図の,緑色の角度です
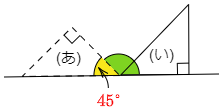
よって,180°-45°を計算して 135°

