課題46【5年生】(こたえ)

　

１　次の計算をしなさい。

10点×4=40(点)

(1)　ガソリン3Lあたり45m走る車があります。5Lのガソリンで何km走りますか。

こたえ

　ガソリン1Lで何km走るかを計算しましょう。
　45÷3＝15(km)　よって1Lあたり15km走ります。
　したがって5Lでは　15×5＝75(km)
　答えは　75km

(2)　秒速340mと時速1200kmではどちらが速いですか。

こたえ

　秒速を時速になおすか，時速を秒速になおすかどちらかです。単位がmとkmと異(こと)なっていますから，その点も注意です。

(秒速を時速になおす場合)
　1分間は60秒，1時間は60分ですから，1時間は60×60＝3600(秒)です。よって1時間に進む距離は
　340×3600＝1 224 000 (m)
です。これをkmになおすと1224km　つまり1時間に1224km進みます。よって早いのは秒速340mの方です。
　答えは　秒速340mの方が速い

(時速を秒速になおす場合)
　1時間は3600秒なので，1200÷3600を計算します。ところがこれは割り切れません。そんなときは分数で表します。
$$1200\div3600=\frac{1200}{3600}=\dfrac{12}{36}=\dfrac13$$

　つまり時速1200kmは，秒速$\dfrac13$kmです。$\dfrac13$kmというのは1kmが1000mですから，1000÷3＝333.33 …(m)です。割り切れませんが，秒速340mとどちらが速いかを比較することはできます。340と333.33 …では340の方が大きいですね。
　答えは　秒速340mの方が速い

(3)　48÷64を分数で表しなさい。約分できるときは約分してください。

こたえ

　48÷64を分数で表すと，$\dfrac{48}{64}$ です。すぐに2で約分できることはわかりますから，$\dfrac{48}{64}=\dfrac{24}{32}$ となります。再び2で約分できそうですが，もう少し大きな数，例えば4でも約分できそうです。しかしもっとよく考えてみると，8でも約分できそうです。$\dfrac{24}{32}=\dfrac34$ これで約分が完了です。
　答えは　$\dfrac34$

(4)　$\dfrac{51}{12}$ を小数で表しなさい。

こたえ

　まずは $\dfrac{51}{12}$ を約分しましょう。3で約分できそうですから $\dfrac{51}{12}=\dfrac{17}4$
　ここからわり算を行います。$\dfrac{17}4=4.25$
　答えは　4.25

２　次の表は，あおぞら小学校とみどり小学校の2つの学校の5年生にペットを飼っているかどうか質問して，飼っていると答えた人数をまとめたものです。

	1組	2組	3組
あおぞら小学校	5	12	7
みどり小学校	9	4	3

　　あおぞら小学校は1クラス25人，みどり小学校は1クラス20人です。クラスの中でペットを飼っていると答えた人の割合が最も多かったのは，どの学校の何組ですか。

10点

こたえ

　表からあおぞら小学校では2組が，みどり小学校では1組が最も人数が多いので，この2つを比べます。
　あおぞら小学校2組：12÷25＝0.48(48%)
　みどり小学校1組：9÷20＝0.45(45%)
　答えは　あおぞら小学校の2組

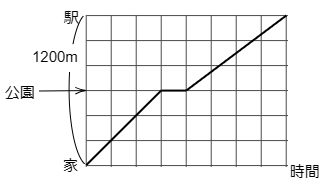
３　あやさんは，家から1200mはなれた駅に向かって歩き出しました。途中公園で2分休けいをとりました。次のグラフはそのときの様子を表しています。

　次の各問いに答えなさい。

10点×3=30(点)

(1)　家から公園までの距離は何mですか。

こたえ

　グラフから公園は家と駅のちょうど真ん中の地点にありますから　1200÷2＝600(m)です。
　答えは　600m

(2)　家から公園までの速さを1としたとき，公園から駅までの速さの割合はいくつですか。

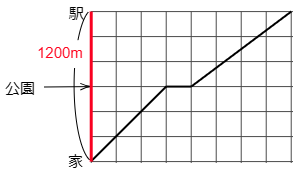
こたえ

　たて6めもり分で1200mですから1めもり分は1200÷6＝200(m)です。一方，横のめもりは，休けい時間が2分であることから1めもり分は2分です。すると家から公園までは2×3＝6(分)で着きましたから，速さは600÷6＝100(m)で毎分100mです。次に公園から駅までは同じく600mで，横のめもりは4つ分ですから2×4＝8(分)かかりました。よって600÷8=75mで毎分75mの速さです。
　よって毎分100mが基準量，毎分75mが比較量ですから
　75÷100=0.75
　答えは　0.75

(3)　あやさんが家を出たのは3時ちょうどでした。あやさんが家を出たちょうどそのとき，駅で買い物を終えたあやさんのお母さんが，自転車で毎分200mの速さで家に向かいました。2人が出会ったのは，3時何分ですか。

こたえ

　グラフにあやさんのお母さんの移動を表す線を書きこみ，あやさんの移動を表す線と交わったところが出会った場所です。お母さんの自転車は毎分200mで走っていますから，1200mを1200÷200=6(分)で進みます。するとお母さんの移動を表す線は図のようになります。

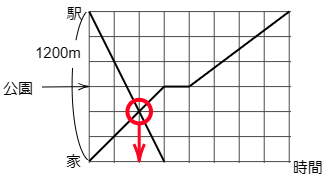
　グラフから横のめもり2つ分のところで2人は出会っています。1めもり分は2分でしたから，2めもりで2×2=4(分)です。
　答えは　3時4分

４　次の各問いに答えなさい。

10点×2=20(点)

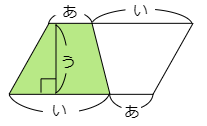
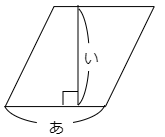
(1)　平行四辺形が図の「あ×い」で表されるのはどうしてかを説明しなさい。

こたえ

　どんな平行四辺形でも，図のように直角三角形を切り取って移動させると長方形の面積になるので「あ×い」で面積を求めることができます。

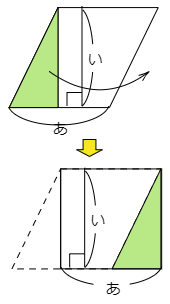
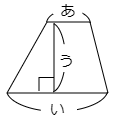
(2)　台形の面積が図の「 (あ＋い)×う÷2」で計算できるのはどうしてかを説明しなさい。

こたえ

　図のように元の台形と合同な図形を，くるっと180°回転させてくっつけると，横の長さが「あ＋い」の平行四辺形ができ上がります。すると(1)の結果から，「(あ＋い)×う」を計算するとこの平行四辺形の面積を求めることができます。元の台形はこの半分ですから，「 (あ＋い)×う÷2」で求めることができます。