１ 次の計算をしなさい。
10点×4=40(点)
(1) $1.2-\dfrac12$
こたえ
$\dfrac12$ は0.5ですから
\[12.-0.5=\underline{\boldsymbol{0.7}}\]
(2) $258.3\div21$
こたえ
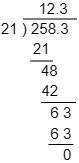
こたえは 12.3
(3) $0.2\times45\div15$
こたえ
考え方その1
頭から計算する，つまり$(0.2\times45)\div15$ を計算します。
\[0.2\times45=9,\ \ 9\div15=\underline{\boldsymbol{0.6}}\]
考え方その2
わり算が1つしかありませんので，わり算から先に計算することができます。つまり $0.2\times(45\div15)$ を計算します。
\[45\div15=3,\ \ 0.2\times3=\underline{\boldsymbol{0.6}}\]
「その2」のやり方は，わり算が連続する計算では使えません。十分注意してください。
(4) 2.3L+421mL は何dLですか。
こたえ
0.1Lが1dLですから，1Lは10dLです。よって，2.3Lは23dLです。
次に，1Lは1000mLですから，10dLが1000mLです。すると1dLは100mL，0.1dLは10ml，0.01dLは1mLです。よって421mLは4.21dLです。
以上により求める答えは
23+4.21=27.21(dL)
２ $2\times2\times2\times2\times\cdots\times2$ という具合に2を20個書いてかけたいったとき，一の位の数は何ですか。
10点
こたえ
２を少しずつかけていき，一の位の数だけを見ていましょう。
\[\begin{align*} &\underline{\boldsymbol{2}}\\[5pt] &2\times2=\underline{\boldsymbol{4}}\\[5pt] &2\times2\times2=\underline{\boldsymbol{8}}\\[5pt] &2\times2\times2\times2=1\underline{\boldsymbol{6}}\\[5pt] &2\times2\times2\times2\times2=3\underline{\boldsymbol{2}}\\[5pt] &2\times2\times2\times2\times2\times2=6\underline{\boldsymbol{4}}\\[5pt] &2\times2\times2\times2\times2\times2\times2=12\underline{\boldsymbol{8}}\\[5pt] &\ \ \ \ \ \vdots \end{align*}\]
一の位の数のだけ書き出してみると
\[2,\ 4,\ 8,\ 6,\ 2,\ 4,\ 6,\ 8,\ \cdots\]
となっています。これは「2,4,8,6」の４つの数のくり返しですね。20回かけと，この4つの数のセットが $20\div4=5$ でちょうど5セット出てきますから，答えは 6 です。
３ あるクラスには26人の児童がいます。このクラスで水泳を習っている児童は10人，絵画を習っている児童は9人，どちらでも習っていない児童は14人でした。
次の問いに答えなさい。
10点×3=30(点)
(1) 水泳と書道の両方を習っている児童は何人ですか。
こたえ
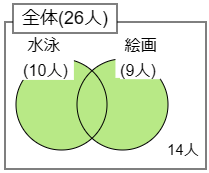
まずは緑色の中に何人いるか計算すると 26-14=12(人)
次に水泳の10人と絵画の9人を足すと 10+9=19(人)
緑色には12人しかいないのですから，はみ出した 19-12=7(人)が水泳と絵画の両方を習っています．答えは 7人
(2) 水泳を習っていて絵画を習っていない人は何人ですか。
こたえ
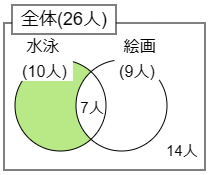
(1)で水泳と絵画の両方を習っている人が7人とわかりましたから，10-7=3(人) 答えは 3人
(3) このクラスで書道を習っている人は21人でした。水泳、絵画、書道の3つとも習っている人は少なくとも何人いますか。
こたえ
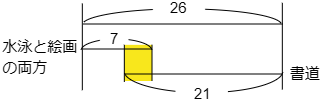
今度は線分部で考えます。3つとも習っている人が最も少なくなる場合を考えるのですから，水泳と絵画の両方の線と，書道の線ができるだけ重ならないようにすると，上の図のようになります。水泳と絵画の両方が7人，書道が21人ですから合計で 7+21=28(人)
ところがクラスは26人ですから 28-26=2(人)
答えは 2人
４ 1辺が10cmの立方体があります。この立方体をAとします。
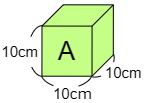
次の問いに答えなさい。
10点×2=20(点)
(1) 図のような直方体の体積は，立方体Aの体積の何倍ですか。
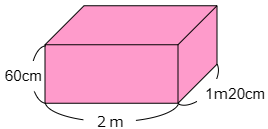
こたえ
立方体の体積は 10×10×10=1000cm3 です。
考え方その1
直方体の体積は
\[200\times120\times60=1440000{\rm cm}^3\]
よって 1440000÷1000=1440
答えは 1440倍
考え方その2
この直方体に立方体Aが何個入るか考えます。
横が2m、つまり200cmですから，200÷10=20。つまり，横には立方体Aを20個ならべることができます。
たては1m20cm、つまり120cmですから，120÷10=12。つまりたてには立方体Aを12個ならべることができます。
高さは60cmですから，60÷10=6。つまり高さには立方体Aを6個ならべることができます。
よって，直方体には立方体Aが横に20個、たてに12個，高さに6個ならべることができますから，直方体全体に立方体Aが入る個数は
$20\times12\times6=1440$(個)
答えは 1440倍
(2) 立方体Aの体積は，次の図のような直方体の体積の何倍ですか。小数で答えなさい。
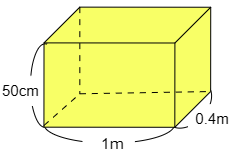
こたえ
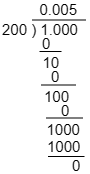
(1)の考え方その2で考えてみます。
この直方体には立方体Aが横に10個，たてに4個、高さに5個入りますから，直方体全体に入る立方体Aの個数は
$10\times4\times5=200$(個)
よって，1÷200=0.005 答えは 0.005倍
