~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の問いに答えなさい。
10点×4=40(点)
(1) $4\dfrac5{12}\times 8$ を帯分数で答えなさい。
(2) $\left(\dfrac{7}{3412}-\dfrac5{6824}\right)\times3412$ を帯分数で答えなさい。
(3) $\left(\dfrac5{204}-\dfrac7{306}\right)\times102$
(4) 1辺の長さが $x$ cmの立方体があります。この立方体よりたてと横の長さがそれぞれ1cm長く,高さが2cm短い直方体の体積を,$x$ を使って表しなさい。
2 りこさんとまなさんは,まだ学校で習っていない分数どうしのかけ算はどのように考えるのか考えてみました。次のに入る数を答えなさい。
りこ「$\dfrac23\times\dfrac57$ はどうやって計算するのかなあ。」
まな「$\dfrac57$ というのは割り算で表すと ① ÷ ② だったよね。」
りこ「そっか、じゃあ $\dfrac23\times\dfrac57$ は
$\dfrac23\times$ ① ÷ ②
って考えればいいってわけね。」
まな「$\dfrac23\times$ ① は, ③ になるね。」
りこ「だから答えは ③ ÷ ② を計算して ④ ね。できたわ!」
10点
3 かなさんは,食塩水について調べました。すると食塩水の濃さは,濃度と呼ばれる次の式で計算されることがわかりました。
濃度(%)$=\dfrac{\mbox{食塩の量}}{\mbox{食塩水の量}}\times100$
食塩水というのは食塩と水の合計ですから,この式は次のように表すこともできます。
濃度(%)$=\dfrac{\mbox{食塩の量}}{\mbox{食塩の量}+\mbox{水の量}}\times100$
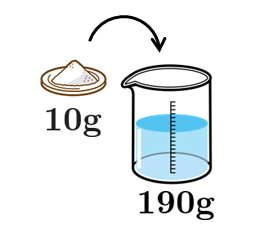
例えば,食塩10gを190gの水に混ぜると200gの食塩水ができますが,この食塩水の濃度は
濃度(%)$=\dfrac{10}{200}\times100=5(\%)$
つまりその食塩水の濃度は5%であるということがわかります。
よって例えば,10%の食塩水が500gあるとき,この食塩水に含まれる食塩の量は 500×0.1=50(g) であることがわかります。
次の各問いに答えなさい。
10点×3=30(点)
(1) 6gの食塩に,何gの水を加えると,4%の食塩水ができますか。
(2) (1)の食塩水に,10gの食塩を混ぜると何%の食塩水になりますか。
(3) (1)の食塩水に,水を50g混ぜると,何%の食塩水ができますか。
4 次の各問いに答えなさい。
10点×2=20(点)
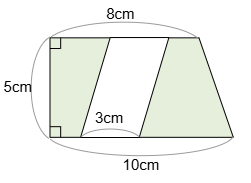
(1) 次の緑色の部分の面積を求めなさい。ただし,中の白色の部分は平行四辺形です。
(2) 正八角形の1つの角の大きさを求めなさい。