4．2つの変量の間の関係(ノート)｜スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅰ　第3章　データの分析

	スライド	ノート
1. データの代表値
2. データの散らばりと四分位範囲
3. 分散と標準偏差
4. 2つの変量の間の関係
5. 仮説検定の考え方

4．2つの変量の間の関係

4.1　散布図

　これまでは1つの変量に対する統計量を見てきたが，ここでは2つの統計量の間に何かしらの関係がないかどうかを調べる方法について見ていく．

　例えば，ある人の身長と体重について，身長を横軸，体重を縦軸にとって，2つのデータを平面上の点として表した次のような図を散布図という．

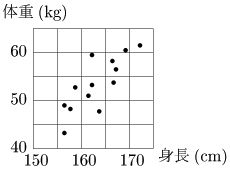
　散布図を見れば，身長と体重の関係性が見えてくる．点は概ね右上がりに分布しているが，このように一方が増加すれば他方も増加するとき，正の相関関係があるという．すなわち身長と体重には正の相関関係があるといえる．逆に一方が増加すれば他方は減少するとき，2つの変量のデータには負の相関関係があるという．この場合，点は右下がりに分布する．また，どちらの関係も認められないとき，相関関係がないという．

4.2　共分散

　2つの変量の相関関係の正負と，その強さを表す統計量を導入する．

　例えば，変量 $x$ を身長，変量 $y$ を体重とし，$n$ 人の身長と体重を

\[(x_1,y_1),\ (x_2,y_2),\ \cdots,\ (x_n,y_n)\]

で表す．平均値をそれぞれ $\overline{x},\overline{y}$ とするとき，偏差の積の平均値，すなわち

を $x$ と $y$ の共分散といい，$s_{xy}$ で表す．

　$i$ 番目の人の $(x_i\!-\!\overline{x})(y_i\!-\!\overline{y})\ $ に注目してみよう．身長，体重ともに平均値より大きい人は $x_i-\overline{x}>0$，$y_i-\overline{y}>0$ となるからそれらの積である $(x_i\!-\!\overline{x})(y_i\!-\!\overline{y})\ $ も正の数となる．同様に，身長，体重ともに平均値より小さい人は負の数どうしを掛けることになるから，このときにも $(x_i\!-\!\overline{x})(y_i\!-\!\overline{y})\ $ は正の数となる．

　一方，身長は平均値よりも大きいが，体重は平均値よりも小さい人は， $x_i-\overline{x}>0$，$y_i-\overline{y}<0$ となるからそれらの積である $(x_i\!-\!\overline{x})(y_i\!-\!\overline{y})\ $ は負の数となる．また，身長が平均値より小さく，体重が平均値より大きい人も負の数と正の数を掛けることになり，このときも $(x_i\!-\!\overline{x})(y_i\!-\!\overline{y})\ $ は負の数となる．

　この一連の考察をまとめると次のような図になる．

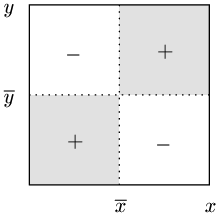
　共分散というのは $(x_i\!-\!\overline{x})(y_i\!-\!\overline{y})\ $ の平均であるから，図のグレーの領域に点が多い場合，すなわち2つの変量について正の相関関係があるとき，$s_{xy}>0$ となるといえる．一方，図の白い領域に点が多い場合，すなわち2つの変量について負の相関関係があるとき，$s_{xy}<0$ となるといえるであろう．

まとめ 　共分散を調べると相関関係の正負がわかる
　　正の相関関係があるとき，正の値をとる
　　負の相関関係があるとき，負の値をとる

4.3　相関係数

　共分散を調べると，相関関係の正負がわかるが，その強さ，すなわち相関の程度まではわからない．

　また，同じデータでも例えば単位をメートルからセンチメートルやミリメートルに変えれば共分散の値も変わるので，共分散の値の大小を見ても，そこから得られる情報は少ない．

　そこで共分散を，標準偏差 $s_x$ と $s_y$ の積で割った量を相関係数といい，$r$ で表す：

相関係数 \[r=\frac{s_{xy}}{s_xs_y}\]

　相関係数には次の特徴がある．

相関係数の特徴 ①　$-1\leqq r\leqq1$
②　強い正の相関関係があるとき，$r$ は $1$ に近い値となる．
　　（散布図は右上がりの直線状に分布）
③　強い負の相関関係があるとき，$r$ が $-1$ に近い値となる．
　　（散布図は右下がりの直線状に分布）
④　直線的な相関関係がないとき，$r$ は $0$ に近い値となる．

発展的補足

※以下の説明では和の記号 $\displaystyle\sum$ が登場する．この記号の意味など詳しくはこちら．

特徴①の証明

　$a_k=x_k-\overline{x}$，$b_k=y_k-\overline{y}$ $(k=1,2,\cdots,n)$ とすると，

\[\begin{align*} s_{xy}&=\frac1n\sum_{k=1}^na_kb_k\\[5pt] s_x&=\sqrt{\frac1n\sum_{k=1}^n{a_k}^2}\\[5pt] s_y&=\sqrt{\frac1n\sum_{k=1}^n{b_k}^2} \end{align*}\]

であるから，

\[\begin{align*} r&=\frac{\displaystyle{\frac1n\sum_{k=1}^na_kb_k}}{\sqrt{\displaystyle{\frac1n\sum_{k=1}^n{a_k}^2}}\sqrt{\displaystyle{\frac1n\sum_{k=1}^n{b_k}^2}}}\\[5pt] &=\frac{\displaystyle\sum_{k=1}^na_kb_k}{\sqrt{\displaystyle\sum_{k=1}^n{a_k}^2}\sqrt{\displaystyle\sum_{k=1}^n{b_k}^2}} \end{align*}\]

と表せる．

　ここで藪から棒だが，任意の実数 $t$ に対して成り立つ次の不等式を持ち出す：

$\displaystyle\sum_{k=1}^n(a_k t -b_k)^2\geqq0\ \cdots$ (あ)

　変形して

$At^2-2Bt+C\geqq0\ \cdots$ (い)

　ただし，

\[A=\sum_{k=1}^n{a_k}^2,\ B=\sum_{k=1}^n{a_k}{b_k},\ C=\sum_{k=1}^n{b_k}^2\]

とおいた．$A, C$ は2乗の和であるから0以上だが，一般のデータにおいては0になることはまずないので正の数としてよい．すると (い) は任意の実数 $t$ について成り立つ $t$ の2次不等式であって，かつ2次の係数が正だから，$At^2+Bt+C=0$ の判別式を $D$ とすると，

$D/4=B^2-AC\leqq0$．

　従って $AC>0$ より

\[\frac{B^2}{AC}\leqq1.\]

　この左辺は $r^2$ を表すから，$r^2\leqq1$．

　故に，$-1\leqq r\leqq 1$．

　等号成立は，(あ)の式を見ればある実数 $t_0$ が存在して，すべての $k$ で $a_kt_0-b_k=0$．すなわち

\[\begin{align*} y_k-\overline{y}&=t_0(x_k-\overline{x})\\[5pt] \therefore \ \ y_k&=t_0x_k-t_0\overline{x}+\overline{y} \end{align*}\]

が成り立つときで，$-t_0\overline{x}+\overline{y}$ は定数だから，それはすべての点$(x_k,y_k)$ が1つの直線上に乗っているときである．

■

特徴 ②，③について

　散布図が一直線上に分布しているとき，相関係数が $1$ や $-1$ となることをもう少し詳細に考察する．

　$a,b$ を定数とする．2つの変量 $x,y$ の間に $y=ax+b$ という関係があるとき，

\[\begin{align*} y_k-\overline{y}&=(ax_k+b)-(a\overline{x}+b)\\[5pt] &=a(x_k-\overline{x}) \end{align*}\]

であるから，

\[\begin{align*} r&=\frac{s_{xy}}{s_xs_y}\\[5pt] &=\frac{\displaystyle{\frac1n\sum_{k=1}^n}(x_k-\overline{x})\cdot a(x_k-\overline{x})}{s_x\cdot |a|s_x}\\[5pt] &=\frac a{|a|}\frac{\displaystyle{\frac1n \sum_{k=1}^n}(x_k-\overline{x})^2}{{s_x}^2}\\[5pt] &=\frac a{|a|}\frac{{s_x}^2}{{s_x}^2}\\[5pt] &=\frac a{|a|}. \end{align*}\]

　従って

　　　$a>0$ のとき，$r=\dfrac aa=1,$
　　　$a<0$ のとき，$r=\dfrac a{-a}=-1.$

■

4.4　分割表

　質的データをとる2つの変量の関係を表にまとめて整理する方法を考える．

例　受験者が60人のある試験で，教材Aを使用したかどうかを調べた結果．

	合	否	計
Aを使用	10	5	15
Aを使用せず	22	23	45
計	32	28	60

　上のような表を分割表，またはクロス集計表という．