3. 　Σ(シグマ)と和の公式(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学B　第2章　数列

	スライド	ノート
1. 等差数列	[無料]
2. 等比数列	[無料]
3. Σ(シグマ)と和の公式	[無料]
4. 階差数列	[会員]
5. 数列の和と一般項	[会員]
6. $a_n=b_n-b_{n-1}$ 型の和	[会員]
7. (等差)×(等比)の和	[会員]
8. 群数列	[会員]
9. 隣接2項間漸化式(その1)	[会員]
10. 隣接2項間漸化式(その2)	[会員]
11. 隣接3項間漸化式	[会員]

3. Σ(シグマ)と和の公式

3.1　和の公式

\begin{align*}&[1]\hspace{4mm} 1+2+3+\cdots+n=\frac12n(n+1)\\[5pt] &[2]\hspace{4mm} 1^2+2^2+3^2+\cdots +n^2=\frac16n(n+1)(2n+1)\\[5pt] &[3]\hspace{4mm} 1^3+2^3+3^3+\cdots +n^3=\left\{\frac12n(n+1)\right\}^2\end{align*}

証明

[1]　右辺は，初項1，公差1の等差数列の，初項から第 $n$ 項までの和であるから，等差数列の和の公式で計算すると右辺になる．

[2]

　$(k+1)^3-k^3=3k^2+3k+1$(恒等式)の利用．

\[\begin{array}{rl} 2^3-1^3=&\!\!\!\!3\cdot1^2+3\cdot1+1\hspace{10mm} (k=1)\\[5pt] 3^3-2^3=&\!\!\!\!3\cdot2^2+3\cdot2+1\hspace{10mm} (k=2)\\[5pt] 4^3-3^3=&\!\!\!\!3\cdot3^2+3\cdot3+1\hspace{10mm} (k=3)\\ &\vdots\\ +\!)(\!n\!+\!1\!)^3\!-\!n^3\!=&\!\!\!\!3n^2\ +\ 3n\ +\ 1\hspace{12mm} (k=n)\\[5pt] \hline (\!n\!+\!1\!)^3\!-\!1^3\!=&\!\!\!\!3(\!1^2\!+\!2^2\!+\!\cdots\!+\!n^2)\!+\!3(\!1\!+\!2\!+\!\cdots\!+\!n\!)\!+\!n\!\cdot\!1 \end{array}\]

　$1^2+2^2+\cdots+n^2$ を $S$ とおくと，

\[(n+1)^3-1=3S+3\cdot\frac12n(n+1)+n\]

\[\begin{align*} \therefore 3S&=(n+1)^3-3\cdot\frac12n(n+1)-(n+1)\\[5pt] &=\frac12(n+1)\{2(n+1)^2-3n-2\}\\[5pt] &=\frac12(n+1)(2n^2+n)\\[5pt] &=\frac12n(n+1)(2n+1)\\[7pt] \therefore S&=\frac16n(n+1)(2n+1) \end{align*}\]

[3]　恒等式 \[(k+1)^4-k^4=4k^3+6k^2+4k*1\] を用いることで，[2]と同様にして示すことができる．

■

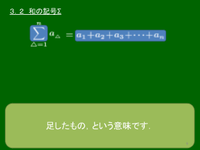
3.2　和の記号Σ

　$\displaystyle \sum_{\triangle=1}^na_{\triangle}$ は \[a_1+a_2+a_3+\cdots +a_n\] を意味する．

例

\[\begin{align*} &\sum_{k=1}^4 a_k=a_1+a_2+a_3+a_4\\[5pt] &\sum_{l=1}^4 a_l=a_1+a_2+a_3+a_4\\[5pt] &\sum_{m=1}^3 (2m\!-\!1)\!=\!(2\!\cdot\!1\!-\!1)\!+\!(2\!\cdot\!2\!-\!1)\!+\!(2\!\cdot\!3\!-\!1)\!=\!9\\[5pt] &\sum_{p=3}^5 2^p=2^3\!+\!2^4\!+\!2^5\!=\!8\!+\!16\!+\!32\!=\!56 \end{align*}\]

和の公式\begin{align*}&[1]\hspace{4mm} \sum_{k=1}^nc=nc\ \ (c\ \mbox{は定数})\\[5pt] &[2]\hspace{4mm}\sum_{k=1}^nk=\frac12n(n+1)\\[5pt] &[3]\hspace{4mm} \sum_{k=1}^n k^2=\frac16n(n+1)(2n+1)\\[5pt] &[4]\hspace{4mm} \sum_{k=1}^n k^3=\left\{\frac12n(n+1)\right\}^2\\[5pt] &[5]\hspace{4mm} \sum_{k=1}^n(2k-1)=n^2\ \ (\mbox{奇数}n\,\mbox{個の和})\end{align*}

3.3　Σの性質

\begin{align*}&[1]\hspace{4mm} \sum_{k=1}^n(a_k+b_k)=\sum_{k=1}^na_k+\sum_{k=1}^nb_k\\[5pt] &[2]\hspace{4mm} \sum_{k=1}^nca_k=c\sum_{k=1}^na_k\ \ (c\, \mbox{は定数}) \end{align*}

証明

[1] \[\begin{align*} \sum_{k=1}^n(a_k+b_k)&=\!(a_1\!+\!b_1)\!+\!(a_2\!+\!b_2)\!+\!(a_3\!+\!b_3)\!+\!\cdots\!+\!(a_n\!+\!b_n)\\[5pt] &=\!(a_1\!+\!a_2\!+\!a_3\!+\!\cdots\!+\!a_n)\!+\!(b_1\!+\!b_2\!+\!b_3\!+\!\cdots\!+\!b_n)\\[5pt] &=\sum_{k=1}^na_k+\sum_{k=1}^nb_k \end{align*}\]

[2] \[\begin{align*} \sum_{k=1}^n ca_k&=\!ca_1\!+\!ca_2\!+\!ca_3\!+\!\cdots\!+\!ca_n\\[5pt] &=\!c\,(a_1\!+\!a_2\!+\!a_3\!+\!\cdots\!+\!a_n)\\[5pt] &=c\sum_{k=1}^n a_k \end{align*}\]

■

例

\[\begin{align*} \sum_{k=1}^4(2k+3)&=\sum_{k=1}^4 2k+\sum_{k=1}^4 3\ \ (\mbox{性質}[1])\\[5pt] &=2\sum_{k=1}^4 k+4\cdot 3\ \ (\mbox{性質}[2])\\[5pt] &=2\cdot\frac12\cdot4(4+1)+4\cdot3\\[5pt] &=\underline{\boldsymbol{32}} \end{align*}\]

\[\begin{align*} \sum_{k=1}^3 k(k+1)&=\sum_{k=1}^3 (k^2+k)\\[5pt] &=\sum_{k=1}^3 k^2+\sum_{k=1}^3 k\ \ \ \ (\mbox{性質}[1])\\[5pt] &=\frac16\cdot3(3+1)(2\cdot3+1)+\frac12\cdot3(3+1)\\[5pt] &=14+6\\[5pt] &=\underline{\boldsymbol{20}} \end{align*}\]

注意

　$\displaystyle\sum_{k=1}^5 k(k+1)=\sum_{k=1}^5k\sum_{k=1}^5(k+1)$ といったような \[\sum_{k=1}^n a_kb_k=\sum_{k=1}^n a_k\sum_{k=1}^n b_k\] は成り立たない．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第2章　数列

	スライド	ノート
1. 等差数列	[無料]
2. 等比数列	[無料]
3. Σ(シグマ)と和の公式	[無料]
4. 階差数列	[会員]
5. 数列の和と一般項	[会員]
6. $a_n=b_n-b_{n-1}$ 型の和	[会員]
7. (等差)×(等比)の和	[会員]
8. 群数列	[会員]
9. 隣接2項間漸化式(その1)	[会員]
10. 隣接2項間漸化式(その2)	[会員]
11. 隣接3項間漸化式	[会員]