中学1年数学 第1章 正の数と負の数
1.1 正の数と負の数
1.2 加法と減法
1.3 加法の計算法則
1.4 乗法と除法
1.5 乗法の計算法則
1.6 四則の混じった計算

6.1 分配法則
乗法・除法は,加法・減法に優先する
加法,減法,乗法,除法の4つをまとめて四則(しそく)といいます。四則が混じった計算には優先順位があることは小学校の時に学びました。乗法と除法が先で,加法と減法があとです。例えば 2+3×4 という計算では乗法を先に計算して 2+12=14 となるのでした。
一方で,この優先順位を変更することも小学校で学習しました。カッコ( )です。カッコを用いると例えば (2+3)×4 という計算は,カッコ内を先に計算して 5×4=20 となるのでした。
小学校で学んだ「分配のきまり」を改めて
ところで,(2+3)×4 という計算は,
2×4+3×4
という具合に,4を分配して計算できました。これを小学校では「分配のきまり」と呼んでいましたが,中学校からは分配法則と呼びます。今の計算では4が後ろから2と3に分配されましたが,
4×(2+3)=4×2+4×3
というように,前から分配することもできます。
分配法則(a+b)×c=a×c+b×ca×(b+c)=a×b+a×c
例題 分配法則を利用して,次の計算をしなさい。
(1) 15×(13−25)
(2) (13−12+14)×12
こたえ
(1) 分配法則より
15×(13−25)=15×13−15×25=5−6=−1_
(2) 分配法則より
(13−12+14)×12=13×12−12×12+14×12=4−6+3=1_
分配法則は分配するだけではない
これも小学校の復習になりますが,分配法則の役割は「分配」だけはありません。分配法則の左辺と右辺を入れ替えてみましょう。
分配法則その2a×c+b×c=(a+b)×ca×b+a×c=a×(b+c)
これはいわば,分配の逆の「まとめる」という役割を果たしていますが,これも分配法則です。「まとめる法則」という用語はありません。
例題 分配法則を利用して,次の計算をしなさい。
(1) 3.14×77+3.14×23
(2) (−32)×25+28×25
こたえ
(1) 分配法則より
3.14×77+3.14×23=3.14×(77+23)=3.14×100=314_
(2) 分配法則より
(−32)×25+28×25=(−32+28)×25=(−4)×25=−100_
6.2 数の集合と四則
数学における集合とは
数学では,範囲がはっきりと決まっているものの集まりを集合といいます。日常会話の集合と違いをはっきりとさせておきましょう。例えばさいころの目の数といえば,1,2,3,4,5,6とその範囲がはっきりしていますから集合といえます。ところが「安いスーパー」というと,同じスーパーでもある人は安いというし,また別の人は安くないということが十分に起こりえます。つまり「安いスーパー」というだけでは数学の集合にはなりません。属しているかいないかを誰もがはっきりと区別することができないからです。
数の集合
ここまでにおいて私たちは,小学校から使ってきた0以上の数から負の数にまで拡張しました。これを集合という見方で整理しておきましょう。
まず数全体という集合の中には,
…,-3,ー2,-1,0,1,2,3,…
という整数の集合が含まれます。そして整数の集合の一部分として正の整数の集合,すなわち
1,2,3,…
という自然数の集合が含まれます。図にまとめておきましょう。
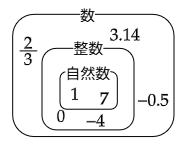
その集合に含まれるいくつかの数が,例として書き込まれている。
同じ集合に属している2つの数で計算すると?
今,集合として
数(全体) 整数 自然数
という3つの集合を考えました。これらの集合において,同じ集合に属している2つの数を用いて四則計算を行うと,その結果も同じ集合に属するか,それともはみ出してしまうのかを考えてみましょう。上の3つのうち,小さい方の集合から見ていきます。
[1] 自然数の集合
- 加法
自然数を自由に2つ選んで足すと,結果はいつでも自然数です。 - 減法
自然数を自由に2つ選んで引くと,例えば5-2ならば3で自然数ですが,2-5はー3ですから自然数ではありません。 - 乗法
自然数を自由に2つ選んで掛けると,結果はいつでも自然数です。 - 除法
自然数を自由に2つ選んで割ると,例えば6÷2ならば3で自然数ですが,2÷6は 13 ですから自然数ではありません。
以上の考察により,いつでも自然数ならば〇,そうでなければ×をつけると次のようにまとめることができます。
| 加法 | 減法 | 乗法 | 除法 | |
| 自然数の集合 | 〇 | × | 〇 | × |
[2] 整数の集合
- 加法
整数を自由に2つ選んで足すと,結果はいつでも整数です。 - 減法
整数を自由に2つ選んで引くと,結果はいつでも整数です。 - 乗法
整数を自由に2つ選んで掛けると,結果はいつでも整数です。 - 除法
整数を自由に2つ選んで割ると,例えば6÷2ならば3で整数ですが,2÷6は 13 ですから整数ではありません。
以上の考察により,いつでも整数ならば〇,そうでなければ×をつけると次のようにまとめることができます。
| 加法 | 減法 | 乗法 | 除法 | |
| 整数の集合 | 〇 | 〇 | 〇 | × |
[3] 数の集合(すべての数の集合)
- 加法
数を自由に2つ選んで足すと,結果はいつでも数です。 - 減法
数を自由に2つ選んで引くと,結果はいつでも数です。 - 乗法
数を自由に2つ選んで掛けると,結果はいつでも数です。 - 除法
数を自由に2つ選んで割ると,結果はいつでも数です。ただし,0で割ることは考えないこととします。
以上の考察により,いつでも数(全体)ならば〇,そうでなければ×をつけると次のようにまとめることができます。
| 加法 | 減法 | 乗法 | 除法 | |
| 数(全体)の集合 | 〇 | 〇 | 〇 | 〇 |
以上の3つをまとめておきましょう。
| 加法 | 減法 | 乗法 | 除法 | |
| 自然数の集合 | 〇 | × | 〇 | × |
| 整数の集合 | 〇 | 〇 | 〇 | × |
| 数(全体)の集合 | 〇 | 〇 | 〇 | 〇 |
補足
数全体の集合は,四則計算が自由に行えます。これを難しい用語を用いて述べると「数全体の集合は四則計算で閉じている」といいます。逆に閉じていないというのはどういうことでしょうか。
自然数しか知らない宇宙人がいたとしましょう。この宇宙人は,加法と乗法はいつでも計算できますが,減法と除法は数字によっては計算できません。2-5といわれても,-3といった負の数を知りませんから「答えはない」となってしまいます。3÷6も同様です。この宇宙人は 12 といった分数を知らないのですから。このとき,自然数の集合は,加法と乗法については閉じていますが,減法と除法については閉じていないという言い方をするのです。
6.3 素因数分解
自然数のうち,1と自分自身しか約数に持たない数を素数(そすう)といいます。ただし1は素数に含めません。1と自分自身しか約数を持たないということは,約数の個数は2です。例えば2の約数は1と2ですから素数です。3の約数は1と3ですから素数です。4の約数は1,2,4の3つあり,1と自分自身(4)の他に2という約数を持っていますから素数ではありません。6も約数が1,2,3,6というように4つあり,1と自分自身(6)以外に2と3という約数をもちますから素数ではありません。素数を小さい方から順に列挙すると
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …
となります。素数は2だけが偶数で,他はすべて奇数です。また素数は無数に存在していることが知られています。
自然数を素数の積に表す
例えば12という自然数は 2×6 と表すことができますが,6は更に 2×3 と表せますから,12は 12=2×2×3 というように表すことができます。そしてこれ以上は細かく積の形に表すことができません。何故ならこのとき使われている数は2と3で,これらは素数だからです。このように自然数を素数だけの積の形で表すことを素因数分解(そいんすうぶんかい)するといいます。素因数分解の例を見ておきましょう。
素因数分解の例
4=22
6=2×3
8=23
10=2×5
12=22×3
14=2×7
15=3×5
16=24
⋮
素因数分解のやり方
ある自然数を素因数分解したときは,図のように,割れる数でどんどん割って,値を小さくしていきます。
例 180
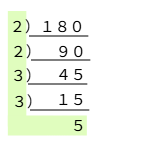
180÷2=90
90÷2=45
45÷3=15
15÷3=5(ここで終わり)
よって180の素因数分解は,緑色の部分にある数を全部掛けて
180=22×32×5
と求めることができます。
補足
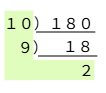
この例では180を小さな素数から順に割っていきましたが,小さな数から順に割る必要はなく,また素数で割る必要もありません。例えば次の図のように計算すると,
180=10×9×2
と表せて,10や9は素数ではないのでこの状態では素因数分解とはいえませんが,10や9なら簡単にそれぞれ 2×5,32と書き直せるので,
180=(2×5)×32×2=22×32×5
というようにして素因数分解ができます。
素因数分解の必要性
中学校の数学を学んでいく上で,素因数分解が必要と感じられる場面の代表が,最大公約数と最小公倍数を考えるときです。
最大公約数を考える場面として分数の約分があります。例えば 120168 という分数を約分することを考えると,これは 120168=24×524×7 と表せることから,24で約分できて 57 となります。ところでこの24というのが120と168の最大公約数で,
120=23×3×5
168=23×3×7
と素因数分解できますから,共通の 23×3 すなわち24が,120と168の最大公約数です。
次に最小公倍数を考える場面としては分数の通分があります。例えば 124+160 という計算は通分,つまり分母を共通にする作業が必要です。24×60の1440で通分しても計算できますが,できるだけ小さな数で通分したいものです。そこで考えるのが24と60の最小公倍数で,
24=23×3
60=22×3×5
と素因数分解されますから,
24=(22×3)×2
60=(22×3)×5
というように共通部分(最大公約数)の 22×3(=12) と,それぞれの残りの部分を掛けて
(22×3)×2×5=120
となり,最小公倍数が120であるとわかります。よってこの分数計算は120で通分すれば簡単で,
124+160=5120+2120=7120
となります。
以上のように,自然数を素因数分解をすることで,最大公約数や最小公倍数が求めやすくなるのです。

