1.正の数と負の数:中学1年数学―オリジナル基礎教科書
中学数学[総目次]
中学1年数学 1章 正の数と負の数
1.正の数と負の数
2.加法と減法
3.加法の計算法則
4.乗法と除法
5.乗法の計算法則
6.四則の混じった計算
検定
教科書

1. はじめに
小学校までは数と言えば0以上の数でした。しかし例えば気温が-5℃だとか,ゲームの得点が-10ポイントになったとか,0より小さな数は日常的にもよく用いられており,その意味も恐らく十分に理解できているのではないでしょうか。
これから中学校の数学を学んでいく過程で,数を少しずつ拡張していきますが,その手始めとして,数の世界を負の数にまで広げていきましょう。
2. 数直線
負の数を導入する前に,次のような数直線(すうちょくせん)というものを説明していきたいと思います。数直線とは「数」を表す「直線」のことです。この直線上の左端に0をとり,そこから均等に目盛りを打って,1,2,3,…と書いていきます。
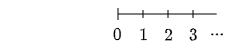
さて今作った数直線には次のような2つの特徴があります。
① 数直線の右側へ行くほど数が大きくなる。
これは数直線を見れば納得できますね。
② どんな数も,数直線上の1点に対応する。
例えば1.5という数は,図の点Aに対応しています。逆に数直線上の点Aは1.5に対応しています。
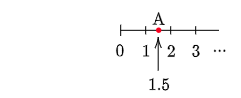
このように,
1.5 $\iff$ 点A
という具合に,1.5という数と,数直線上の点Aは完全に対応しています。これは1.5だけにとどまりません。あらゆる数が,数直線上の1点に対応しており,逆に数直線上の1点は,ある数に対応しているのです。つまり
「数」と,数直線上の「点」は,1対1に対応している
のです。この事実は誠に大切です。なぜかというと,
数直線によって,数を目で見える形で捉えることができるから
です。少しわかりにくいですね。それではこの点についてもう少し詳しくお話しておきましょう。

今話題にしている「1」とか「2」とかといった数は,よく考えるととても不思議な存在です。
「1個」「2個」とか,あるいは「1メートル」「2メートル」とか,日常で数を用いるときには,具体的に何か物を数えたり,長さを測ったりする場合がほとんどです。
でも,ただ「1」や「2」と言うだけでは,具体的な形や物があるわけではありません。
そこで役に立つのが数直線です。数直線では「1」や「2」を直線上の点として表します。数直線を使うと,形のないものが,直線上の1点として形をもつようになります。そして,右に行けば大きく,左に行けば小さくなる――これが,数の大小関係という性質です。
このように,数直線は,数の性質を目で見てはっきりと理解できるようにしてくれるのです。
3. 負の数
0より小さな数を負の数(ふのすう)といい,「-(マイナス)」の記号(負の符号といいます)を使って表します。例えば0より1だけ小さい数が $-1$ で,$-1$ より $1$ だけ小さい数が$-2$,さらに $1$ だけ小さい数が $-3$,… のように表します。また,0より $1.5$ だけ小さい数が $-1.5$ で,0より $\dfrac12$ だけ小さい数が $-\dfrac12$ です。
これまで使ってきた0より大きな数を正の数(せいのすう)といいます。こちらは「+(プラス)」 の記号(正の符号といいます)を使って表すこともありますが,省略されることがほとんどです。
「+」と「-」の記号をまとめて符号(ふごう)といいます。
0という数は,正の数と負の数の境界になっていますが,0は正の数でも負の数でもないとすると決められています。つまり数というのは,次の3つのいずれかに分けられます。
① 正の数 ② 負の数 ③ 0
数直線を拡張する
先ほど導入した数直線は,0から右側にどんどん書いていったものでした。
これからは,その数直線を左側にも伸ばして,負の数も書いていきましょう。
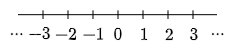
数直線上で,0を表す点を原点(げんてん)といいます。
こうして数直線を広げることで,負の数も含めた数全体の特徴をみていきます。
実は,ここで大事なのは,上で説明した2つの特徴がそのまま使えるということです。つまり,
① 数直線の右側へ行くほど数が大きくなる。
② どんな数も,数直線上の1点に対応する。
の2つです。
まず①について。$-3$ より $-2$ の方が大きく,$-2$ より $-1$の方が大きく,$-1$ より0の方が大きいことになります。
次に②について。例えば $-1.5$ は次の数直線上の点Bに対応します。逆に数直線上の点Bは $-1.5$ に対応しています。
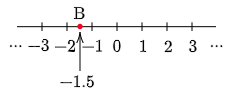
このように数を負の数に拡張したあとでも
「数」と,数直線上の「点」は,1対1に対応している
ということがいえるのです。つまり,負の数を含めた数全体も,数直線を使えば目で見える形としてとらえることができるのです。こうした「数を目でとらえる考え方」を大切にすれば,このあとの学習でのつまずきもきっと少なくなるに違いありません。
●絶対値
数直線において,ある数が対応する点と,原点との距離を「||」という記号を使って表します。例えば,$2$ を表す点と原点との距離は2ですから
\[|\,2\,|=2\]
と書き表します。同じように,$-2$ を表す点と原点との距離も2です。

よって
\[|\,-2\,|=2\]
と書き表します。
一般に $|a|$ と書いて「$a$ の絶対値(ぜったいち)」と読みます。書くときの注意として,例えば $|\,2\,|$ と書いたとき,数字の $1$ を含む $121$(百二十一) とまぎれないように,2本の縦線をまっすぐに引きましょう。
●整数と自然数
小学校では 0,1,2,3,… を整数と言っていましたが,これからは
\[\cdots,\ -3,\ -2,\ -1,\ \ 0,\ \ 1,\ \ 2,\ \ 3,\ \ \cdots\]
というように,小学校で整数と呼んでいた数に,負の記号「−」がついた負の数も加えて整数といいます。
また,正の整数,つまり 1,2,3,… を自然数(しぜんすう)といいます。この「自然数」という用語は,これからの学習でよく登場します。

演習1 次の数直線で,点A,B,Cに対応する数を答えなさい。
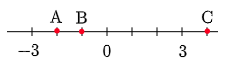
こたえ
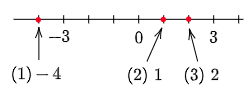
演習2 次の数に対応する点を,数直線に示しなさい。
(1) -4 (2) 1 (3) 2
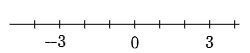
こたえ
演習3 次の数の絶対値を答えなさい。
(1) ー3.14 (2) $-\dfrac85$ (3) 0 (4) 53
こたえ

中学数学[総目次]
中学1年数学 1章 正の数と負の数
1.正の数と負の数
2.加法と減法
3.加法の計算法則
4.乗法と除法
5.乗法の計算法則
6.四則の混じった計算
検定
教科書