3.加法の計算法則:中学1年数学―オリジナル基礎教科書
中学数学[総目次]
中学1年数学 1章 正の数と負の数
1.正の数と負の数
2.加法と減法
3.加法の計算法則
4.乗法と除法
5.乗法の計算法則
6.四則の混じった計算
検定
教科書

1. 加法の計算法則
例えば,
$(+2)+(+3)$ と
$(+3)+(+2)$
は,どちらも答えが $+5$ になります。また,
$(-2)+(+3)$ と
$(+3)+(-2)$
も,どちらも答えが $+1$ になります。
このように加法,すなわち足し算では,計算の順番を変えても答えが同じになります。この計算の順番を交換できる決まりを加法の交換法則(こうかんほうそく)といいます。小学校では「交換のきまり」と呼んでいましたね。
次に,
$\{(+2)+(+3)\}+(+4)$ と
$(+2)+\{(+3)+(+4)\}$
は,どちらも答えが $+9$ になります。また
$\{(+2)+(-3)\}+(-4)$ と
$(+2)+\{(-3)+(-4)\}$
も,どちらも答えが $-5$ になります。
このように,加法では,カッコのつけ方を変えても,答えは同じになります。この計算の優先順位を変更できる決まりを加法の結合法則(けつごうほうそく)といいます。小学校では「結合のきまり」と呼んでいたものです。
加法の計算法則 [1] 加法の交換法則 $a+b=b+a$
[2] 加法の結合法則 $(a+b)+c=a+(b+c)$

減法には交換法則や結合法則はないの?
例えば,$2-3$ は $-1$ となり,$3-2$ は $1$ となりますから,減法では交換法則が成り立ちません。
また,$(2-3)-4$ は $-5$ となり,$2-(3-4)$ は $3$ となりますから,減法では結合法則も成り立ちません。
これで減法では交換法則も結合法則も成り立たないことがわかりました。
ところが,ちょっと工夫すると,交換法則や結合法則が利用できるようになります。その工夫とは?
減法を加法に書きかえる
例えば,$(+2)-(+3)$ という計算は数直線上において,$+2$ から左向きに 3 だけ進んだ点が表す $-1$ となります。この左向きというのが減法の記号「-」からきている訳ですが,これを「右向き進め」を意味する加法の記号「+」に変えることができます。それには「左向きに3だけ進む」を「右向きに $-3$ だけ進む」としてやればよいのです。
$(+2)-(+3)$ → $(+2)+(-3)$
もう1つ例を見ておきましょう。$(+2)-(-3)$ は数直線上の $+2$ から左向きに$-3$ だけ進むことを意味し,これを右向きに $3$ だけ進むと言いかえることができます。
$(+2)-(-3)$ → $(+2)+(+3)$
このように,減法の記号「-」を加法の記号「+」に変える代わりに,記号のすぐ後ろの数の符号を変えることで,どんな減法も加法によって表すことができるのです。

2. 加法と減法の混じった式
式をシンプルにする
負の数というものを考え始めてから,正の数には $+2$ や $+5$ といったように,正の符号「+」を付けてきました。
これによって正の数であることがはっきりした一方で,小学校では $5+2$ と書いていたものが $(+5)+(+2)$ となったり,$5-2$ が $(+5)-(+2)$ といったように長くなり,なんだか書きにくくなりました。数が2つだけなまらまだしも,
$(+5)-(+3)-(-7)+(-2)$
という式だともう書くのもイヤになります。この表現を,小学校のときのようにシンプルに書いてはいけないのでしょうか?
その答えは,書いてもよい!です。
この点について,以下で詳しく見ていきましょう。
「項」とは
式を小学校のときのようにシンプルに表現するには,少し用語の準備が必要です。
例 $(+5)-(+3)-(-7)+(-2)$
この式を加法だけの式にすると
$(+5)+(-3)+(+7)+(-2)$
となります。
加法だけの式における $+5$,$-3$,$+7$,$-2$ を,この式の項(こう)といいます。
正の数である $+5$ と $+7$ を正の項,負の数である $-3$ と $-2$ を負の項といいます。
この式には正の項と負の項を合わせて4つの項がありますから「項数は 4 である」という言い方もします。
いよいよ核心部分――項を並べた式
実は,加法だけの式においては,加法の記号である「+」を省略して,項だけを並べた式にすることができるのです!
ポイント
加法の記号「+」を省略して,項を並べた式にできる
例えば,$(+5)+(-3)+(+7)+(-2)$ の場合,次のようになります。

このとき,式の先頭の項が正の数ならば,その数だけは正の符号である「+」を省略することができます。この例では $+5$ が $5$ になっている部分がそれです。
これで小学校のときと同じ表現になりました!これからはメンドウな $(+5)+(-3)+(+7)+(-2)$ という表現はやめにして,$5-3+7-2$ とシンプルに書くことにしましょう。
例題 17-58+23-62
こたえ
考え方① 前から順番に計算する
17-58=-41
-41+23=-18
-18-62=-80
答えは -80
考え方② 交換法則や結合法則を利用
これは $17$,$-58$,$+23$,$-62$ という4つの項を並べた式です。これらの項と項の間には,次のように加法の記号「+」が省略されています。
17-58+23-62
=(+17)+(-58)+(+23)+(-62)
よって,加法の交換法則が使えます。中央の2つを入れ替えると良さそうです。
17-58+23-62
=17+23-58-62
更に,加法の結合法則を使って前2つと,後ろ2つをそれぞれ計算します。
(17+23)+(-58-62)
あとはこれを計算して
40-120=-80
答えは -80
加法の交換法則と結合法則を,この「項」という用語を用いて説明すると次のようになります。
ポイント
加法においては
- どの2つの項も交換可能
- どの2つの項とも結合可能
項の見つけ方
交換法則や結合法則を使って計算の工夫をするためには,1つ1つの項を手早く見つけ出せるようにしておくと便利です。
項を並べた式(つまり加法の記号「+」が省略された式)では,「+」や「-」の記号は,すぐ後ろの数とセットにして考えるというのがポイントです。
「+」や「-」の記号は,すぐ後ろの数とセットにして考える

注意
$7-(-4)$ のように,「-」が連続するところがある場合には,$7+4$ と変形してから考えます。この場合の項は,$+7$ と $+4$ の2つです。

発展的補足
項を探すとき,「+」や「-」の記号は,すぐ後ろの数とセットにして考えると述べましたが,この点について詳しく説明しておきましょう。
(+17)+(-58)+(+23)+(-62) のような,加法だけの式では,加法の記号「+」とカッコを省略して,項を並べた式で表すことができるのでした。次のアニメーションを見てください。
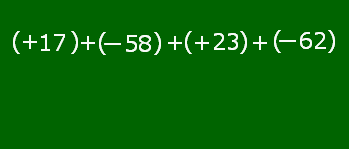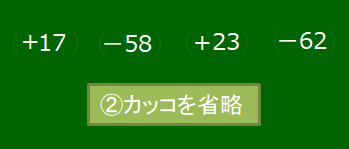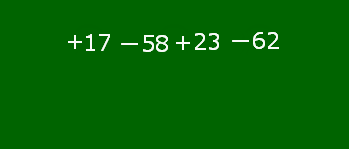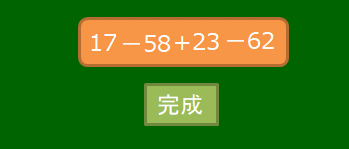
これを元の状態に戻すと,次のアニメーションのようになります。
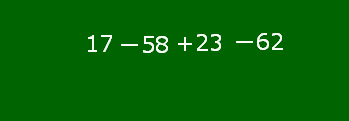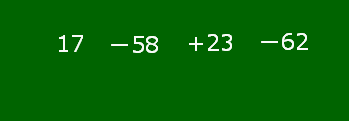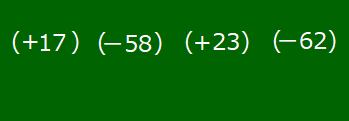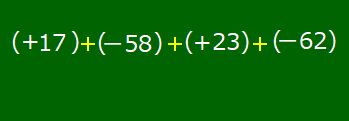
「17-58+23-62」が加法だけの式になるまでの変化の様子
このように考えると,項を並べた式における正の符号「+」や負の符号「-」が,すぐ後ろの数とセットになることが理解できると思います。
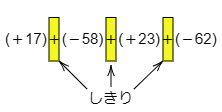
「+」という記号には,加法を表す意味と,正の数であることを示す符号の意味の2つがあることは,前節のコラム で述べました。複数の項からなる式において,加法の意味の「+」は,式を項に分けるしきりとみなすこともできるのです。

演習1 次の計算をしなさい。
(1) 5-8+13-2
(2) -4+15+3-16
(3) 10+(-3)-(-6)
(4) 8.1-3.4-(-1.7)
(5) $\dfrac76+\left(-\dfrac43\right)-\left(-\dfrac32\right)$
(6) $-2-\left(–\dfrac92\right)-\left(+\dfrac{14}3\right)$
こたえ

中学数学[総目次]
中学1年数学 1章 正の数と負の数
1.正の数と負の数
2.加法と減法
3.加法の計算法則
4.乗法と除法
5.乗法の計算法則
6.四則の混じった計算
検定
教科書
