4.乗法と除法:中学1年数学―オリジナル基礎教科書
中学数学[総目次]
中学1年数学 1章 正の数と負の数
1.正の数と負の数
2.加法と減法
3.加法の計算法則
4.乗法と除法
5.乗法の計算法則
6.四則の混じった計算
検定
教科書

0. はじめに
小学校では,新しい計算を習うとき,まず身近な例で考えてきました。例えば,2×3 なら「あめを1人に2個ずつ配ります。3人に配るとき,あめは何個必要でしょう?」というように,絵や物のイメージで考えることが多かったですね。
中学校では,「負の数」を使った掛け算や割り算も学びます。掛け算はこれまでと同じように具体例で考えられることもありますが,割り算になると少しイメージが難しいことも出てきます。
中学校の数学は,少しずつ「具体的な話」から「考え方のルール」に進んでいくのが特徴です。これは新しい世界に入るようなもので,最初は戸惑うかもしれません。でも,ルールを一度受け入れてしまえば,いろいろな計算がスムーズにできるようになります。
例えばこのあと習う「負の数どうしを掛けると正の数になる」というルール。最初は「なんでそうなるの?」と思うかもしれません。理由はいくつかの例で説明できますが,ひとまず「こういう計算のルールなんだ」と受け入れて覚えてしまうのも1つの方法です。そうすれば,あとで理由を学んだときに「なるほど!」とスッキリしやすくなります。
1. 乗法
掛け算のことを乗法(じょうほう)といいます。
例えば 2×3 の答えは6ですが,6をこの乗法の積(せき)といいます。
さっそく結論から
負の数も含めた数どうしの乗法(掛け算)の考え方について,まずは結論をお伝えします。なぜそうなるのかは,のちほど数直線を用いてやさしく説明します。
乗法(掛け算)のやり方
1.2つの数の絶対値でかけ算を行う
(絶対値の積は当然,正の数)
2.答えの符号を決める
- 2数が同符号なら,答えは正
(正の数)×(正の数) → (正の数)
(負の数)×(負の数) → (正の数) - 2数が異符号なら,答えは負
(正の数)×(負の数) → (負の数)
(負の数)×(正の数) → (負の数)
例
- $(-6)\times(-3)$
$|-6|=6,\ |-3|=3$ → $6\times3=18$
$-6$ も $-3$ も負の数だから,同符号
答えは $\boxed{18}$ - $(-8)\times4$
$|-8|=8,\ |4|=4$ → $8\times4=32$
$-8$ は負の数, $4$ は正の数だから,異符号
答えは $\boxed{-32}$

発展的補足
乗法(掛け算)がどうして上のように計算されるのでしょうか?
数直線を使って掛け算のしくみを見ていきましょう。数直線を使うと,正の数や負の数でも,場所や方向のイメージで計算ができます。
●正の数を掛ける
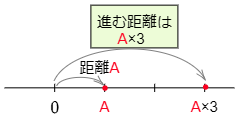
例えば,ある数Aに,正の数3を掛ける計算であるA×3の場合,数直線を用いて次のように計算します。
正の数を掛けるときの手順
数直線で,原点OからAまでの距離と向きを調べる。
(距離は常に0以上,向きは右なら正,左なら負)
→Aと同じ向きに,原点からAまでの距離の3倍進む。
→止まったところの数が答え。
例1 (-2)×3
数直線で,原点から-2までは,距離が2で左向き。
→この向きのまま,距離を3倍(2×3=6)にして進む。
→止まった場所は −6。
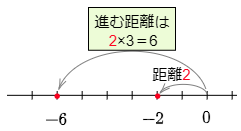
答えは -6
(-2)×3の具体例
- 1日に気温が2℃ずつ下がります。3日後,気温は何℃変わっていますか?
こたえ:6℃下がっている(計算結果:−6℃) - 1日にあめを2個ずつ食べます。3日で何個減っていますか?
こたえ:6個減っている(計算結果:−6個)
例2 (-2)×0.5
数直線で,原点から-2までは,距離が2で左向き。
→この向きのまま,距離を0.5倍(2×0.5=1)にして進む。
→止まった場所は −1。
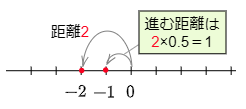
答えは -1
(-2)×0.5の具体例
- 水槽の水が1日に2cmずつ減ります。半日後、何cm減っていますか?
こたえ:1cm減っている
(計算結果:−1cm) - ゲームで体力が1時間に2ポイント減ります。30分後、何ポイント減っていますか?
こたえ:1ポイント減っている
(計算結果:−1ポイント)
●負の数を掛ける
例えば,ある数Aに負の数-3を掛ける計算であるA×(-3)の場合,数直線を用いて次のように計算します。
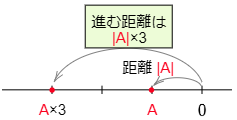
負の数を掛けるときの手順
数直線で,原点からAまでの距離と向きを調べる。
→Aの向きと逆向きに,原点からAまでの距離の3倍進む。
→止まったところの数が答え。
このように,負の数を掛けるということは,加法や減法のときがそうであったように,向きが逆転すると理解しておくと間違いがありません。
ポイント負の数を掛ける → 進む向きが逆転
例3 2×(-3)
数直線上で,原点から2までは,距離が2で右向き。
→逆の左向きに,距離を3倍(2×3=6)にして進む。
→止まった場所は −6。
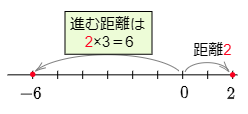
答えは -6
2×(-3)の具体例
- 東向きに毎秒2mで歩く人がいます。3秒前は、現在地から見てどこにいましたか?
こたえ 西に6mの地点
(計算結果:−6m) - 植物が毎日2mmずつ伸びます。3日前は現在と比べて何mm長かったですか?
こたえ 6mm短かった。
(計算結果:−6mm)
例4 (-2)×(-3)
数直線上で,原点からの-2までは,距離が2で左向き。
→逆の右向きに,距離を3倍(2×3=6)にして進む。
→止まった場所は 6。
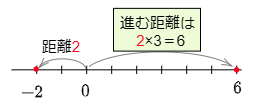
答えは 6
(-2)×(-3)の具体例
- 1日に温度が2℃ずつ低くなっていきます。3日前の温度は,現在と比べてどうでしたか。
こたえ 6℃高い - 1日にあめを2個ずつ食べます。3日前の個数は,現在と比べてどうでしたか
こたえ 6個多い
2. 除法
割り算のことを除法(じょほう)といいます。
例えば,6÷2 の答えは3ですが,3をこの除法の商(しょう)といいます。
ここでは負の数も含めた割り算を考えていきましょう。
乗法(掛け算)のときと同じように,なぜそうなるのかはあと回しにして,とにかく負の数も含めた除法(割り算)ができるようになりましょう。
さっそく結論から
除法(割り算)のやり方
1.2つの数の絶対値で割り算を行う。
(答えは当然,正の数)
2.答えの符号を決める
- 2数が同符号なら,答えは正
(正の数)÷(正の数) → (正の数)
(負の数)÷(負の数) → (正の数) - 2数が異符号なら,答えは負
(正の数)÷(負の数) → (負の数)
(負の数)÷(正の数) → (負の数)
例
- $(-15)\div(-3)$
$|-15|=15,\ |-3|=3$ → $15\div3=5$
$-15$ も $-3$ も負の数だから,同符号
答えは $\boxed5$ - $(-8)\div4$
$|-8|=8,\ |4|=4$ → $8\div4=2$
$-8$ は負の数, $4$ は正の数だから,異符号
答えは $\boxed{-2}$

発展的補足
除法(割り算)の意味とは
それでは除法(割り算)の計算が,なぜ上のようになるのかを説明していきましょう。
6÷2 の答えは3です。つまり 6÷2=3 です。
このとき,6=2×3 が成り立ちます。
実は,これがとても大事な関係なのです。
6÷2=3 が正しいとき,6=2×3 も正しい。
逆に,6=2×3 が正しいとき,6÷2=3 も正しい。
6÷2=3 $\iff$ 6=2×3
つまり除法には,2つの考え方があるのです。
- 1つは,これまで通り「いくつずつに分けられるか」という考え方。
- そしてもう1つは「何を掛けたらこの数になるか?」というかけ算からの考え方。
例えば $6\div2$ なら,「6を2つに分けるといくつずつか?」と考えてもいいし,「2に何をかけたら6になるか?」と考えることもできます。
そして,負の数を含んだ除法を理解するには,「掛け算から考える」方法が,とても役に立つのです。
このように,割り算を掛け算になおすことで,計算の意味をより深く理解できるようになります。
※この考え方は,高校生になったとき,文字式を文字式で割るというところでも生きてきます。意欲的な方はこちら をどうぞ。
ポイント除法は乗法から
●正の数で割る
例1 (-6)÷2
(-6)÷2の答えを□とすると
(-6)÷2=□ → 2×□=-6
よって □=-3
答えは -3
例2 (-6)÷0.5
(-6)÷0.5の答えを□とすると
(-6)÷0.5=□ → 0.5×□=-6
よって □=-12
答えは -12
●負の数で割る
例3 6÷(-2)
6÷(-2)の答えを□とすると
6÷(-2)=□ → -2×□=6
よって □=-3
答えは -3
例4 6÷(-0.5)
6÷(-0.5)の答えを□とすると
6÷(-0.5)=□ → (-0.5)×□=6
よって □=-12
答えは -12
例5 (-6)÷(-2)
(-6)÷(-2)の答えを□とすると
(-6)÷(-2)=□ → (-2)×□=-6
よって □=3
答えは 3
3. 0を含む除法(割り算)の考え方
● 0を割る
0÷2の答えが□だとすると,
0÷2=□ → 2×□=0
よって □=0
このように0を,0でない数 $a$ で割ると,$a\times\square=0$ から□は常に0となります。
● 0で割る
2÷0の答えが□だとすると,
2÷0=□ → 0×□=2
この□に当てはまる数はありません。0にどんな数を掛けても0になり,決して2になることはありません。
まとめ
0を含む除法
- 0÷(0でない数)=0
- どんな数も「0で割る」ことはできない

問題1 次の計算をしなさい。
(1) (+5)×(+4)
(2) (+3)×(-3)
(3) (-8)×7
(4) (-10)×(-6)
こたえ

問題2 次の計算をしなさい。
(1) (+12)÷(+4)
(2) (+8)÷(-2)
(3) (-14)÷7
(4) (-20)÷(-5)
こたえ

中学数学[総目次]
中学1年数学 1章 正の数と負の数
1.正の数と負の数
2.加法と減法
3.加法の計算法則
4.乗法と除法
5.乗法の計算法則
6.四則の混じった計算
検定
教科書
