高校数学[総目次]
数学Ⅱ 第1章 式と証明
| スライド | ノート | |
| 1. 整式の除法 | [無料] | |
| 2. 分数式 | [無料] | |
| 3. 恒等式 | [無料] | |
| 4. 等式の証明 | [無料] | |
| 5. 不等式の証明 | [無料] |
1. 整式の除法
1.1 商と余り
2つの整式 $A, B$ について,
$A=BQ\ \ \cdots$ ①
となる整式 $Q$ が存在するとき,
$A$ は $B$ で割り切れる
といい,$Q$ を商という.
例
$x^2-2x-3=(x+1)(x-3)$
よって,$x^2-2x-3$ は $x+1$ で割り切れ,そのときの商は $x-3$ である.
「$\boldsymbol{A}$ が $\boldsymbol{B}$ で割り切れない」とは,①を満たす $Q$ がないときで,このとき
$A=BQ+R$
ただし,$\boldsymbol{(B}$ の次数$\boldsymbol{)>(R}$ の次数$\boldsymbol{)}$
を満たす $Q$ と $R$ が一意的に定まる.
この $Q$ を $A$ を $B$ で割ったときの商,$R$ を余りという.
例
$2x^3+x-3=(x^2+2x-1)(2x-4)+11x-7$
よって,$2x^3+x-3$ を $x^2+2x-1$(2次式) で割ったときの商は,$2x-4$,余りは $11x-7$(1次式)
1.2 筆算による整式の除法
例
(1) $(x^3-x^2+x-2)\div(x-2)$
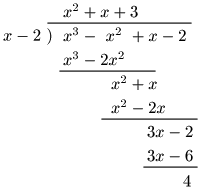
よって,商 $x^2+x+3$,余り $4$
(2) $(2x^3+x-3)\div(x^2+2x-1)$
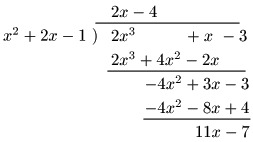
よって,商 $2x-4$,余り $11x-7$
補足
慣れてくれば,係数のみ書き出すのでよい.例えば上の(1)は次のようにする:
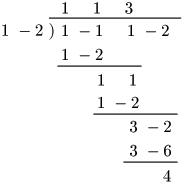
1.3 組立除法
割る式が1次の式ならば,次の組立除法と呼ばれる計算方法もある:
例(1)
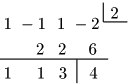
注意
割る式の1次の係数が1でないときには注意を要する.
例 $(2x^3-5x^2+8x+2)\div(2x-1)$
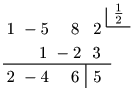
\[\begin{align*} 2x^3\!-\!5x^2\!+\!8x\!+\!2&=\left(\!x\!-\!\frac12\!\right)(2x^2\!-\!4x\!+\!6)\!+\!5\\[5pt] &=\left(\!x\!-\!\frac12\!\right)\cdot2(x^2\!-\!2x\!+\!3)+5\\[5pt] &=(2x-1)(x^2-2x+3)+5 \end{align*}\]
よって,商 $x^2-2x+3$,余り $5$
このページで疑問は解決されましたか?
こちらから数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第1章 式と証明
| スライド | ノート | |
| 1. 整式の除法 | [無料] | |
| 2. 分数式 | [無料] | |
| 3. 恒等式 | [無料] | |
| 4. 等式の証明 | [無料] | |
| 5. 不等式の証明 | [無料] |

