3. 極形式(ノート)
基礎をスライドで学ぶ

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート
1. 複素平面	[無料]
2. 複素数が表す図形	[無料]
3. 極形式	[会員]
4. ド・モアブルの定理	[会員]
5. 複素数と図形	[会員]

3. 極形式

3.1　極形式とは

　複素平面上の点 $z$ を，Oからの距離 $r$ と，実軸の正の向きからの角 $\theta$ で表すことを考える：

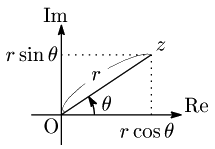
　図より， \[z=r\cos\theta+i\,r\sin\theta\] \[\therefore z=r(\cos\theta+i\sin\theta)\] 　複素数のこのような表し方を極形式という．

極形式 \[ z=r(\cos\theta +i\sin\theta)\]

　このときの角 $\theta$ を偏角といい，${\rm arg}\,z$ で表す．

\[ r=|z|,\ \ \theta ={\rm arg}\, z \]

補足

　例えば，${\rm arg}\,(1-i)$ は $\dfrac 74\pi$ でも $-\dfrac\pi4$ でもよい．つまり，$2\pi$ の整数倍の差がある2つを同一視する．
　${\rm arg}\,z_1={\rm arg}\,z_2$ というときは，$2\pi$ の整数倍の違いを無視して一致することを意味する．

例

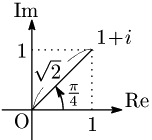
　$z=1+i$ のとき，$|z|=\sqrt2$，${\rm arg}\,z=\dfrac\pi4$ により， \[z=\sqrt2\left(\cos\frac\pi4+i\sin\frac\pi4\right)\]

定理　$z$ が実数　　$\iff$「${\rm arg}\ z=0$ or $\pi$」又は $z=0$
　$z$ が純虚数　$\iff$　${\rm arg}\ z=\dfrac\pi 2$ or $\dfrac 32\pi$

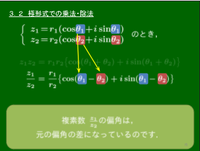
3.2　複素数の乗法・除法

　$z_1=r_1(\cos\theta_1+i\sin\theta_1)$，$z_2=r_2(\cos\theta_2+i\sin\theta_2)$ とすると，

\[\begin{align*} z_1z_2&=r_1r_2(\cos\theta_1+i\sin\theta_1)(\cos\theta_2+i\sin\theta_2)\\[5pt] &=r_1r_2\{\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2)\\ &\hspace{15mm}+i(\sin\theta_1\cos\theta_2+\cos\theta_1\sin\theta_2)\}\\[5pt] &=r_1r_2\{\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\} \end{align*}\]

であるから，

\[\begin{align*} |z_1z_2|&=|r_1r_2|\sqrt{\cos^2(\theta_1+\theta_2)+\sin^2(\theta_1+\theta_2)}\\[5pt] &=|r_1||r_2|\\[5pt] &=|z_1||z_2|\\[8pt] {\rm arg}\,(z_1z_2)&={\rm arg}z_1+{\rm arg}z_2 \end{align*}\]

　同様に，

\[\begin{align*} \frac{z_1}{z_2}&=\frac{r_1(\cos\theta_1+i\sin\theta_1)}{r_2(\cos\theta_2+i\sin\theta_2)}\\[5pt] &=\frac{r_1}{r_2}\cdot\frac{(\cos\theta_1+i\sin\theta_1)(\cos\theta_2-i\sin\theta_2)}{(\cos\theta_2+i\sin\theta_2)(\cos\theta_2-i\sin\theta_2)}\\[5pt] &=\frac{r_1}{r_2}\cdot\frac {(\cos\theta_1+i\sin\theta_1)(\cos\theta_2-i\sin\theta_2)}1\\[5pt] &=\frac{r_1}{r_2}\cdot(\cos\theta_1+i\sin\theta_1)(\cos\theta_2-i\sin\theta_2)\\[5pt] &=\frac{r_1}{r_2}\cdot\{(\cos\theta_1\cos\theta_2+\sin\theta_1\sin\theta_2)\\ &\hspace{20mm}+i(\sin\theta_1\cos\theta_2-\cos\theta_1\sin\theta_2)\}\\[5pt] &=\frac{r_1}{r_2}\{\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\} \end{align*}\]

であるから，

\[\begin{align*} &\left|\frac{z_1}{z_2}\right|=\left|\frac{r_1}{r_2}\right|=\frac{|r_1|}{|r_2|}=\frac{|z_1|}{|z_2|}\\[5pt] &{\rm arg}\left(\frac{z_1}{z_2}\right)=\theta_1-\theta_2={\rm arg}\,z_1-{\rm arg}\,z_2 \end{align*}\]

まとめ\begin{align*}
|z_1z_2|&=|z_1|\,|z_2|\\
{\rm arg}\ (z_1z_2)&={\rm arg}\ z_1+{\rm arg}\ z_2\\
\\
\left|\frac{z_1}{z_2}\right|&=\frac{|z_1|}{|z_2|}\\
{\rm arg}\left(\frac{z_1}{z_2}\right)&={\rm arg}\ z_1-{\rm arg}\ z_2
\end{align*}

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート
1. 複素平面	[無料]
2. 複素数が表す図形	[無料]
3. 極形式	[会員]
4. ド・モアブルの定理	[会員]
5. 複素数と図形	[会員]