5. 複素数と図形(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート	問題
1. 複素平面	[会員]
2. 複素数が表す図形	[会員]
3. 極形式	[会員]		[会員]
4. ド・モアブルの定理	[会員]
5. 複素数と図形	[会員]

5. 複素数と図形

5.1　線分の内分点，外分点

　平面ベクトルのときと全く同じ考え方により，複素平面での内分点，外分点は次のように表される：

2点A$(\alpha)$，B$(\beta)$ について，線分ABを $$\begin{align*} &m:n \mbox{に内分する点}:　\frac{n\alpha+m\beta}{m+n}\\ &m:n \mbox{に外分する点}:　\frac{-n\alpha+m\beta}{m-n} \end{align*}$$

補足

[ベクトルでは次のようであった．]

　${\rm A}(\overrightarrow{\mathstrut a})$，${\rm B}(\overrightarrow{\mathstrut b})$ について，線分ABを

　　$m:n$ に内分する点の位置ベクトル：$\dfrac{n\overrightarrow{\mathstrut a}+m\overrightarrow{\mathstrut b}}{m+n}$
　　$m:n$ に外分する点の位置ベクトル：$\dfrac{-n\overrightarrow{\mathstrut a}+m\overrightarrow{\mathstrut b}}{m-n}$

5.2　方程式の表す図形

円

　円とは，中心と呼ばれる1点から等しい距離にある点の集合であるから，その方程式は次のように表される：

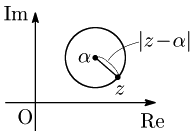
　点 $\alpha$ を中心とする半径 $r$ の円の方程式 $$\begin{align*} &|z-\alpha|=r\\ \iff &(z-\alpha)(\overline{z}-\overline{\alpha})=r^2\\ \iff &z\overline{z}-\overline{\alpha}z-\alpha\overline{z}=r^2-|\alpha|^2 \end{align*}$$

垂直二等分線

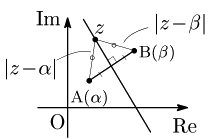
　線分ABの垂直二等分線とは，線分ABの両端から等しい距離にある点の集合であるから，その方程式は次のように表される：

　A$(\alpha)$，B$(\beta)$ のとき，線分ABの垂直二等分線の方程式 $$|z-\alpha|=|z-\beta|$$

5.3 半直線のなす角

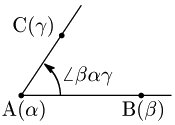
　図において，半直線ABからACまでの回転角を $$\angle \beta\alpha\gamma$$ で表す．極形式 での偏角と同様に，反時計回りの回転角を正の向き，時計回りを負の向きとする．

　極形式のところで学んだ，${\rm arg}\dfrac{z_1}{z_2}={\rm arg}\,z_1-{\rm arg}\,z_2$ を上の場合に適用することを考えよう．${\rm A}(\alpha)$ が極Oにくるような平行移動を考えたとき，点${\rm B}(\beta),\ {\rm C}(\gamma)$ は，それぞれ点${\rm B}'(\beta’),\ {\rm C}'(\gamma’)$ に移ったとすると，

$\left\{\begin{array}{l}\beta’=\beta-\alpha\\[5pt] \gamma’=\gamma-\alpha\end{array}\right.$　…①

である．

よって

$$\begin{align*} \angle\beta\,\alpha\,\gamma&=\angle\beta’\,0\,\gamma’\\[5pt] &={\rm arg}\,\gamma’-{\rm arg}\,\beta’\\[5pt] &={\rm arg}\,\dfrac{\gamma’}{\beta’}\\[5pt] &={\rm arg}\,\dfrac{\gamma-\alpha}{\beta-\alpha}\ \ (\because\mbox{①}) \end{align*}$$

となる．

　異なる3点 $\alpha,\ \beta,\ \gamma$ について， $$\angle \beta\alpha\gamma={\rm arg}\,\frac{\gamma -\alpha}{\beta -\alpha}$$

注意

　文字の順番に注意．$\angle\gamma\alpha\beta$ だと角の大きさは上の図と同じだが，向きが逆になる．

異なる3点が1直線上にあるための条件

　　異なる3点 $\alpha,\beta,\gamma$ が1直線上

　$\iff \angle\beta\alpha\gamma=0$ 又は $\pi$

　$\iff {\rm arg}\dfrac{\gamma-\alpha}{\beta-\alpha}=0$ 又は $\pi$

　$\iff \dfrac{\gamma-\alpha}{\beta-\alpha}$ は実数

垂直条件

　${\rm A}(\alpha)$，${\rm B}(\beta)$，${\rm C}(\gamma)$ について，

　　　AB⊥AC

　$\iff \angle\beta\alpha\gamma=\dfrac\pi2$ 又は $-\dfrac\pi2$

　$\iff {\rm arg}\dfrac{\gamma-\alpha}{\beta-\alpha}=\dfrac\pi2$ 又は $-\dfrac\pi2$

　$\iff \dfrac{\gamma-\alpha}{\beta-\alpha}$ は純虚数

【発展】4点が同一円周上にあるための条件

　異なる4点 ${\rm A}(\alpha)$，${\rm B}(\beta)$，${\rm C}(\gamma)$，${\rm D}(\delta)$ のうち，どの3点も同一直線上にないとする．つまりこの4点を使って四角形ができる場合である．このとき，この4点が同一円周上にあるための条件を求めよう．

　この4点のうち，CとDは直線ABに関して同じ側にあるか，反対側にあるかどちらかである．

1°　CとDが直線ABに関して同じ側にあるとき

　円周角の定理 ，及び円周角の定理の逆 により

2°　CとDが直線ABに関して反対側にあるとき

　円に内接する四角形 の条件により

　1°，2° により，次が成り立つ：

---

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート	問題
1. 複素平面	[会員]
2. 複素数が表す図形	[会員]
3. 極形式	[会員]		[会員]
4. ド・モアブルの定理	[会員]
5. 複素数と図形	[会員]