指数の拡張と累乗根の性質をスライドでやさしく解説

高校数学[総目次]

数学Ⅱ　第5章　指数関数・対数関数

	スライド	ノート	問題
1. 指数の拡張
2. 指数関数
3. 対数とその性質
4. 対数関数
5. 常用対数

1．指数の拡張

　これまでに学んだのは $5^2$ や $a^4$ など，指数部分が自然数であった．例えばこれらは

\[5^2=5\times5,\hspace{5mm} a^4=a\times a\times a\times a\]

を意味しており，$n$ を自然数として $a^n$ というのは「$a$ を $n$ 回掛ける」のであった．ここで指数 $n$ を

自然数 → 整数 → 有理数 → 実数

へと拡張することを考える．まずは「自然数 → 整数」の拡張から始めよう．

1.1　0や負の整数の指数

5⁰ や 3^-2 は何を意味するのか

　$a\neq0$ とする．$a^0$ や $a^{-2}$ を考えていくのであるが，「$a$ を0回掛ける」や「$a$ を $-2$ 回掛ける」では意味が通らない．ではこれらの数をどのように取り決める(定義する)のがよいだろうか．

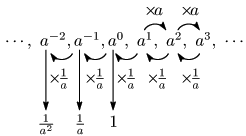
　$a^2$ から $a^3$ へと指数が1だけ増加すると，数は $a$ 倍された．逆に，$a^3$ から $a^2$ へと指数を1だけ小さくすると，数は $\dfrac1a$ 倍される．この規則を $a(=a^1)$ から $a^0$ の場合にも適用すると，$a^1$ を $\dfrac 1a$ 倍したものが $a^0$ だと考えて

\[a^0=a^1\times\frac1a=1\]

とするのが自然であろう．更に $a^0(=1)$ から $a^{-1}$ の場合についても

\[a^{-1}=a^0\times\frac1a=1\times\frac1a=\frac1a\]

と考えることができる．

　このように考えて，0や負の整数の指数を次のように定義する．

定義　$a\neq0,\ n$ が正の整数のとき，\[a^0=1,\ a^{-n}=\frac1{a^n},\ \left(\mbox{特に，}a^{-1}=\frac1a\right)\]

例

(1) $5^0=1$
(2) $3^{-2}=\dfrac1{3^2}=\dfrac19$
(3) $(-2)^{-3}=\dfrac1{(-2)^3}=\dfrac1{-8}=-\dfrac18$
(4) $0.2^{-3}=\left(\dfrac15\right)^{-3}=\dfrac1{\left(\frac15\right)^3}=5^3=125$

1.2　整数の指数法則

拡張しても指数法則はすべて成り立つ

　これまで自然数であった指数を，整数にまで拡張したが，拡張したあとであってもこれまで成り立っていた指数法則はすべて成り立つ．(本当のところは指数法則が成り立つように，0や負の整数の指数を定義したのである．）

　$a\neq0,\ b\neq0$ で，$m,\ n$ が整数のとき，\begin{align*} &[1]\ a^ma^n=a^{m+n}\\[5pt] &[2]\ (a^m)^n=a^{mn}\\[5pt] &[3]\ (ab)^n=a^nb^n\\[5pt] &[4]\ \frac{a^m}{a^n}=a^{m-n}\\[5pt] &[5]\ \left(\frac ab\right)^n=\frac{a^n}{b^n} \end{align*}

例
　$[1]\ \ a^2a^{-3}=a^2\cdot\dfrac1{a^3}=\dfrac1a=a^{-1}=a^{2-3}$
　$[2]\ \ (a^2)^{-3}=\dfrac1{(a^2)^3}=\dfrac1{a^6}=a^{-6}=a^{2\cdot(-3)}$
　$[3]\ \ (ab)^{-2}=\dfrac1{(ab)^2}=\dfrac1{a^2b^2}=a^{-2}b^{-2}$

1.3　累乗根

$a$ の $n$ 乗根とは何か

　$a$ の $n$ 乗根は，方程式 $x^n=a$ の解である．

例
　$9$ の2乗根（平方根ともいう）
　　　$x^2=9$ より $x^2-9=0$
　　　$\therefore (x+3)(x-3)=0$
　　　よって，$3$ と $-3$
　$8$ の3乗根（立方根ともいう）
　　　$x^3=8$ より $x^3-8=0$
　　　$\therefore (x-2)(x^2+2x+4)=0$
　　　よって，$２$ と $\ -1+\sqrt3i$ と $-1-\sqrt3i$
　$-8$ の3乗根
　　　$x^3=-8$ より $x^3+8=0$
　　　$\therefore (x+2)(x^2-2x+4)=0$
　　　よって，$-2$ と $\ 1+\sqrt3i$ と $1-\sqrt3i$
　$16$ の4乗根　　　
　　　$x^4=16$ より $x^4-16=0$
　　　$\therefore (x^2-4)(x^2+4)=0$
　　　よって，$2$ と $-2$ と $2i$ と $-2i$

補足

①　2乗根，3乗根，4乗根，… をまとめて累乗根(るいじょうこん)という．
②　複素数の範囲で考えると，一般に $a\neq0$ のとき，$a$ の $n$ 乗根は $n$ 個ある．(ただし重解も2個，3個，…というように区別して数える．)

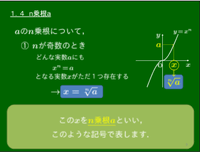
1.4　$n$ 乗根 $a$

「$n$ 乗根 $a$」と「$a$ の $n$ 乗根」は違うもの

　前節で「$a$ の $n$ 乗根」というものを学んだが，これに似た用語に「$n$ 乗根 $a$」がある．これらは異なるものなので気を付けなければならない．

　$a$ の $n$ 乗根について，$n$ が奇数のときと偶数のときで場合分けする．

1．$\boldsymbol{n}$ が奇数のとき

　$y=x^3,\ y=x^5,\ y=x^7,\ \cdots$ といった関数のグラフは，概ね次のような形をしている：

　このグラフを見ると，どんな実数 $a$ にも $y$ の値が $a$ となるような実数 $x$，すなわち $x^n=a$ となる $x$ がただ1つだけ存在していることがわかる．この $x$ を\[\sqrt[n]{a}\]と書き表し，「 $\boldsymbol{n}$ 乗根 $\boldsymbol{a}$ 」と読む．

例1　$8$ の3乗根は，$2$ と $-1\pm\sqrt3i$
　　よって，$2$ を $\sqrt[3]8$ と書き，
　　　　「3乗根8」
　　と読む：
　　　　$\sqrt[3]8=2$
例2　$-8$ の3乗根は，$-2$ と $1\pm\sqrt3i$
　　よって，$-2$ を $\sqrt[3]{-8}$ と書き，
　　　　「3乗根$-8$」
　　と読む：
　　　　$\sqrt[3]{-8}=-2$

2．$\boldsymbol{n}$ が偶数のとき

　$y=x^2,\ y=x^4,\ y=x^6,\ \cdots$ といった関数のグラフは，概ね次のような形をしている：

　このグラフをもとに，$y=a$ のときの $x$ について，$a>0$， $a=0$， $a<0$ に分けて考える．

(i) $a > 0$ のとき
　$x^n=a$ となる $x$ が正負1個ずつある．その正の方を　$\sqrt[n]a$ で表し，「 $\boldsymbol{n}$ 乗根 $\boldsymbol{a}$ 」と読む．そして負の方を $-\sqrt[n]a$ で表し，「 マイナス $\boldsymbol{n}$ 乗根 $\boldsymbol{a}$ 」と読む．
(ii) $a=0$ のとき
　　　　$\sqrt[n]0=0$
(iii) $a < 0$ のとき
　　　　$\sqrt[n]a$ は存在しない．
例　$16$ の4乗根は，
　　　$2$ と $-2$ と $2i$ と $-2i$．
　　　よって，

　$2$ を $\sqrt[4]{16}$ と書き「4乗根16」と読む．
$-2$ を $-\sqrt[4]{16}$ と書き「マイナス4乗根16」と読む．

よくある間違い　$\sqrt[4]{16}=\pm2$ (←正しくない．)

補足

　$2$ 乗根 $a$ は，通常左上の $2$ を省略する：

\[\sqrt[2]a\ \to \ \sqrt a\]

　また，「$2$ 乗根 $a$」や「平方根 $a$」とは呼ばず，「ルート $\boldsymbol{a}$」と呼ぶのが通例である．

重要な注意

　$\boldsymbol{a>0}$ のとき，$\sqrt[n]a$ は，その定義から $n$ の偶奇にかかわらず正の数である：

　この事実は，次節「1.5　累乗根の性質」で利用される．

1.5　累乗根の性質

$\sqrt2\times\sqrt3=\sqrt6$ といった計算は累乗根でもできる

　ここでは $\sqrt[n]a$ の $a$ を正の数に制限する．そうすることで直前の「重要な注意」でも述べたように，$\sqrt[n]a$ は $n$ の偶奇にかかわらず，ただ1つの正の数を表すということがいえる．この事実を用いると，平方根で成り立っていた以下の性質がそのまま一般の累乗根でも成り立つ．