高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [無料] | |
| 2. 指数関数 | [無料] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |

4.対数関数
4.1 対数関数
$a$ が正であって1でない数であるとき,$y=a^x$ は $x(>0)$ の値が1つ決まればそれに応じて $y$ の値がただ1つ決まった.すなわち $y$ は $x$ の関数である.大事なことはこの対応が1対1であるということだ.
$y=a^x$ の $x$ と $y$ は1対1対応
つまり先に $y$ の値を決めても,その値に応じて $x$ の値はただ1つ定まるのであるから $x$ は $y$ の関数である.この性質は指数関数の単調性によっている.
例 $y=2^x$
$x=0$ のとき $y=1$.逆に $y=1$ のとき $x=0$.
$x=1$ のとき $y=2$.逆に $y=2$ となる $x=1$.
$x=2$ のとき $y=4$.逆に $y=4$ となる $x=2$.
$\vdots$
任意の正の実数 $y$ に対して,$y=a^x$ を満たす $x$ を $\log_ay$ と書き表した.つまり $x=\log_ay$ である.しかし数学では通常先に決める方の文字を $x$,それに伴って決まる数を $y$ とすることが多いので,
\[y=\log_ax\]
と書き表すのである.
対数関数とは
$a > 0,a\neq1$ のとき,
\[y=\log_a x\]
を,$\boldsymbol{a}$ を底(てい)とする $\boldsymbol{x}$ の対数関数という.

4.2 対数関数のグラフ
対数関数 $y=\log_ax$ のグラフはどのようになっているのであろうか.対数の値がわかり易い $x$ の値でいくつか調べたものを表にまとめて、それら $(x,y)$ の組を座標平面に書き入れて滑らかに連結してみよう.
例1 $y=\log_2x$
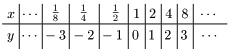
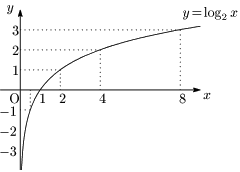
例2 $y=\log_{\frac12}x$
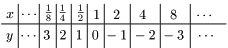
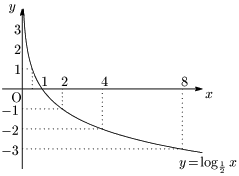
底が,$2$ と $\dfrac12$ の2つだけを調べたが,共通点と相違点は何であろうか.
共通点は,いずれのグラフも $y$ 軸の右側にあるということだ.つまり $\boldsymbol{x}$ は正の値しかとらない.一方 $\boldsymbol{y}$ は実数全体をとっている.また,2つのグラフは共に点 $\boldsymbol{(1,0)}$ を通っている.更に2つのグラフは共に $y$ 軸にどんどん近付いている.このように遠いところにおいて限りなく近付いていく直線を漸近線という.2つのグラフは共に $\boldsymbol{y}$ 軸が漸近線である.最後に上の2つのグラフは合同(平行移動・回転移動・対称移動で重なる)である.
相違点は,$y=\log_2x$ は右上がり,$y=\log_{\frac12}x$ は右下がりである.これは決定的で重要な相違点である.ではそのような違いを生じさせる $a$ の値の範囲はどうなっているのか?それは
$a>1$ と $0<a<1$
である.この違いがグラフの形,すなわち関数の特徴を決定付けるのである.
上の考察のうちのいくつかは次の節で再び確認することになるが,とりあえずグラフの形や通る点についてまとめると次のようになる.
対数関数 $\boldsymbol{y=\log_ax}$ のグラフ
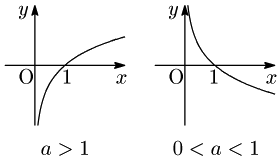
- $a>1$ のとき, 右上がりの曲線
$0<a<1$ のとき,右下がりの曲線 - 点 $(1,0)$ を通る
- $y$ 軸が漸近線
対数関数と指数関数のグラフの関係
次に,対数関数と指数関数のグラフの関係を確認していこう.
例として $y=2^x$ を考える.例えば点$(3, 8)$ はこの指数関数のグラフ上の点だが,$x$ 座標と $y$ 座標を入れ替えた点 $(8, 3)$ は対数関数 $y=\log_2x$ のグラフ上の点である.これは何も点 $(3,8)$ に限ったことではなく,指数関数 $y=2^x$ のグラフ上のあらゆる点 $(a,b)$ について,その $x$ 座標と $y$ 座標を入れ替えた点 $(b, a)$ は対数関数 $y=\log_2x$ のグラフ上の点である.すなわち
点 $(a,b)$ が指数関数 $y=2^x$ のグラフ上の点
$\iff$ 点 $(b,a)$ が対数関数 $y=\log_2x$ のグラフ上の点
が成り立つ.この考察から,指数関数のグラフと対数関数のグラフは直線 $y=x$ に関して対称であることがわかる.
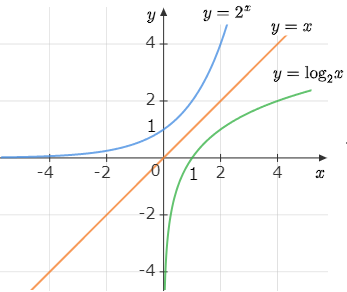
指数関数と対数関数のグラフの関係
指数関数 $y=a^x$ と対数関数 $y=\log_ax$ のように,底が同じ数 $a$ であるグラフは直線 $y=x$ に関して対称である.
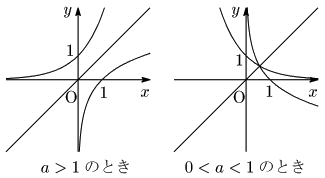

4.3 対数関数の性質
すぐ上で見たように,対数関数 $y=\log_ax$ のグラフにより,次のことがわかる:
対数関数の性質
対数関数 $y=\log_ax$ について
- 定義域と値域
定義域:正の実数全体
値 域:実数全体 - 単調性
$a>1$ のとき単調に増加する.すなわち
$p<q\iff\log_ap<\log_aq$
$0<a<1$ のとき単調に減少する.すなわち
$p<q\iff\log_ap>\log_aq$
補足
[2]により,
が成り立つ.(対数方程式で利用.)
例題1 $\log_5\sqrt{10}$ と $\log_53$ の大小関係を調べよ.
こたえ
解答例を表示する >例題2 $\log_3x+\log_3(x-8)=2$ を解け.
こたえ
解答例を表示する >例題3 $\log_{\frac13}(x-1)>-1$ を解け.
こたえ
解答例を表示する >
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [無料] | |
| 2. 指数関数 | [無料] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |