5. 常用対数(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第5章　指数関数・対数関数

	スライド	ノート
1. 指数の拡張	[無料]
2. 指数関数	[無料]
3. 対数とその性質	[会員]
4. 対数関数	[会員]
5. 常用対数	[会員]

5．常用対数

5.1　常用対数とは

　10を底とする対数を常用対数という．常用対数の応用は専ら自然数の桁数に関する問題と，小数第 $n$ 位の数字に関する問題である．$\log_{10}x$ のいくつかの値がどんな数学Ⅱの教科書の巻末にも表としてまとめられている．

5.2　常用対数の応用1（桁数）

　例えば，2桁の自然数といえば10以上99以下の自然数のことを指す．$n$ を自然数として式で表すと，$10\leqq n<100$ である．すると対数関数の単調性により，この各辺の常用対数をとると，底の10が1より大きいので不等号の向きを保存したまま　$\log_{10}10\leqq \log_{10}n<\log_{10}100$，すなわち

\[1\leqq\log_{10}n<2\]

となる．

ここで「$n<100$」としたことに注意しておこう．「$n\leqq 99$」では常用対数をとると $\log_{10}99$ となってしまい，簡単な式にはならない．

　これで2桁の自然数 $n$ の常用対数 $\log_{10}n$ がもれなく1以上2未満の数になることがわかった．逆に $\log_{10}n$ の値が1以上2未満になるような自然数 $n$ はすべて2桁の自然数である．すなわち

$n$ が2桁の自然数 $\iff 1\leqq\log_{10}n<2$

がいえる．これは対数関数の単調性からいえるのであって，下のグラフを見れば，より理解が深まるであろう．自然数 $n$ の桁数が，常用対数をとることで求められるのは，この同値な言いかえができることによっている．

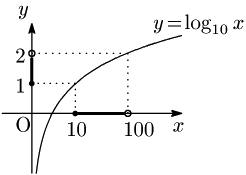
　一般に次が成り立つ：

念のための注意

　$\log_{10}n$ の値が「$1.\cdots$」となった場合，この1につられて $n$ を1桁の数と判断してはいけない．$10^1(=10)$ は2桁の数， $10^2(=100)$ は3桁の数である．

例題1　$5^{30}$ の桁数を求めよ．ただし，$\log_{10}2=0.3010$ とする．

答

　解答例を表示する >

\[\begin{align*} \log_{10}5^{30}&=30\log_{10}5\\[5pt] &=30\log_{10}\frac{10}2\\[5pt] &=30(\log_{10}10-\log_{10}2)\\[5pt] &=30(1-0.3010)\\[5pt] &=20.97 \end{align*}\] 　よって， \[20\leqq \log_{10}5^{30} < 21\] \[\therefore \log_{10}10^{20}\leqq \log_{10}5^{30} < \log_{10}10^{21}\] 　底の10は1より大きいから， \[10^{20}\leqq 5^{30} < 10^{21}\] 　よって $5^{30}$ は21桁の数．

5.3　常用対数の応用2（小数第 $n$ 位）

　0と1の間の数で，小数第2位に初めて0以外の数字が現れる数 $p$ を考えよう．具体的には 0.023 や 0.0514 などである．これらの数はもれなく $0.01\leqq p<0.1$ の範囲に含まれている．すると対数関数の単調性により，この各辺の常用対数をとると，底の10が1より大きいから不等号の向きが保存されて $\log_{10}0.01\leqq \log_{10}p<\log_{10}0.1$，すなわち

$-2\leqq \log_{10}p<-1\ \ \cdots$ ①

となる．逆に①の関係を満たす $p$ はすべて小数第2位に初めて0以外の数字が現れる．すなわち

$p$ は小数第2位に初めて0以外の数 $\iff -2\leqq\log_{10}p<-1$

がいえる．この辺りの事情は常用対数を用いて自然数の桁数を考えたときと全く同じで，対数関数の単調性からいえることであり，下のグラフを見れば理解が深まる．

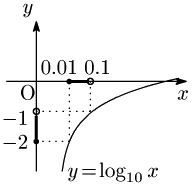
　一般には次が成り立つ：

念のための注意

　$\log_{10}p$ の値が「$-1.\cdots$」となった場合，$p$ は小数第2位に初めて0以外の数が現れる数であるということである．$10^{-2}(=0.01)$ は小数第2位に初めて0以外の数が現れる最小の数であり，$10^{-1}(=0.1)$ は小数第1位に初めて0以外の数が現れる最小の数である．

例題2　$0.5^{10}$ は小数第何位に初めて0でない数字が現れるか．ただし，$\log_{10}2=0.3010$ とする．

答

　解答例を表示する >

　$0.5=\dfrac12=2^{-1}$ より，$\log_{10}0.5=\log_{10}2^{-1}=-\log_{10}2$ となるから， \[\begin{align*} \log_{10}0.5^{10}&=10\log_{10}0.5\\[5pt] &=10\times(-\log_{10}2)\\[5pt] &=-3.010 \end{align*}\] 　よって， \[-4\leqq\log_{10}0.5^{10} < -3\] \[\log_{10}10^{-4}\leqq\log_{10}0.5^{10} < \log_{10}10^{-3}\] 　底の10が1より大きいから， \[10^{-4}\leqq 0.5^{10} < 10^{-3}\] 　よって $0.5^{20}$ は 小数第4位 に初めて0以外の数が現れる．

5.4　常用対数の応用3（最高位の数）

　5.1節で常用対数を用いることで自然数の桁数が計算できることがわかった．しかし実はもっと詳細な情報も常用対数を用いて得ることができるのである．その1つが最高位の数である．例えば，3桁の数789の最高位の数は7であり，5桁の数98765の最高位の数は9であるが，この7とか9といった数字を常用対数を利用して求めることができる．ただしそのためには，予めその数の常用対数の値がわかっていなければならない．（わかっていない場合はそれを計算するところから始めなければならない．）

例題3　$5^{30}$ の最高位の数を求めよ．ただし，$\log_{10}2=0.3010,\ \log_{10}3=0.4771$ とする．

答

　解答例を表示する >

　5.2節の例題の結果から，$5^{30}$ が21桁の数であることがわかったので，その最高位の数を $a(=1,2,\cdots,9)$ とすると， \[a\times10^{20}\leqq 5^{30} < (a+1)\times10^{20}\] と表せる．各辺の常用対数をとると， \[\log_{10}a+20\leqq \log_{10}5^{30} < \log_{10}(a+1)+20\] 　中辺の $\log_{10}5^{30}$ は $20.97$ であったから， \[\log_{10}a+20\leqq 20.97 < \log_{10}(a+1)+20\] 　各辺から20を引くと， \[\log_{10}a\leqq 0.97 < \log_{10}(a+1)\] 　ここで，$\log_{10}9=2\log_{10}3=0.9542$，$\log_{10}(9+1)=1$ であるから，$a=9$．
　よって，$5^{30}$ の最高位の数は 9 ．

5.5　常用対数の応用4（小数第 $n$ 位の数）

　5.3節において，0と1の間の実数 $p$ が小数第何位で初めて0でない数字が現れるかを常用対数を用いて計算する方法を見た．しかし実はもっと詳細な情報も常用対数を用いて得られるのである．その1つが初めて0ではない数が現れたときその数字が何であるかということである．例えば，小数第2位に初めて0でない数字が現れる例として，$0.023$ や $0.0514$ があるが，これらの2や5といった数字を常用対数を利用して求めることができる．ただしそのためには，予め $\boldsymbol{\log_{10}p}$ の値がわかっていなければならない．（わかっていない場合はそれを求めるところから始めなければならない．）

例題4　例題2で$0.5^{10}$ は小数第4位に初めて0でない数字が現れることがわかったが，その数字を求めよ．ただし，$\log_{10}2=0.3010,\ \log_{10}3=0.4771$ とする．

答

　解答例を表示する >

　5.3節の例題の結果から，$0.5^{10}$ が小数第4位で初めて0でない数字が現れる数であることがわかったので，小数第4位の数を $a(=1,2,\cdots,9)$ とすると， \[a\times10^{-4}\leqq 0.5^{10} < (a+1)\times10^{-4}\] 　各辺の常用対数をとると， \[\log_{10}a-4\leqq \log_{10}0.5^{10} < \log_{10}(a+1)-4\] 　5.3節において，中辺の $\log_{10}0.5^{10}$ は $-3.010$ であるとわかったから， \[\log_{10}a-4\leqq -3.010 < \log_{10}(a+1)-4\] 　各辺に4を加えて， \[\log_{10}a\leqq 0.99 < \log_{10}(a+1)\] 　ここで，$\log_{10}9=2\log_{10}3=0.9542$，$\log_{10}(9+1)=1$ であるから，$a=9$．
　よって，$0.5^{10}$ の小数第4位の数は 9 ．

---

高校数学[総目次]

数学Ⅱ　第5章　指数関数・対数関数

	スライド	ノート
1. 指数の拡張	[無料]
2. 指数関数	[無料]
3. 対数とその性質	[会員]
4. 対数関数	[会員]
5. 常用対数	[会員]