高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [無料] | |
| 2. 指数関数 | [無料] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |

1.指数の拡張
これまでに学んだのは $5^2$ や $a^4$ など,指数部分が自然数であった.例えばこれらは
\[5^2=5\times5,\hspace{5mm} a^4=a\times a\times a\times a\]
を意味しており,$n$ を自然数として $a^n$ というのは「$a$ を $n$ 回掛ける」のであった.ここで指数 $n$ を
自然数 → 整数 → 有理数 → 実数
へと拡張することを考える.まずは「自然数 → 整数」の拡張から始めよう.
1.1 0や負の整数の指数
$a\neq0$ とする.$a^0$ や $a^{-2}$ を考えていくのであるが,「$a$ を0回掛ける」や「$a$ を $-2$ 回掛ける」では意味が通らない.ではこれらの数をどのように取り決める(定義する)のがよいだろうか.
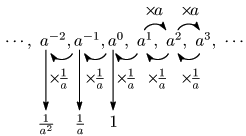
$a^2$ から $a^3$ へと指数が1だけ増加すると,数は $a$ 倍された.逆に,$a^3$ から $a^2$ へと指数を1だけ小さくすると,数は $\dfrac1a$ 倍される.この規則を $a(=a^1)$ から $a^0$ の場合にも適用すると,$a^1$ を $\dfrac 1a$ 倍したものが $a^0$ だと考えて
\[a^0=a^1\times\frac1a=1\]
とするのが自然であろう.更に $a^0(=1)$ から $a^{-1}$ の場合についても
\[a^{-1}=a^0\times\frac1a=1\times\frac1a=\frac1a\]
と考えることができる.
$a\neq0$ のとき,
このように考えて,0や負の整数の指数を次のように定義する.
定義 $a\neq0,\ n$ が正の整数のとき,\[a^0=1,\ a^{-n}=\frac1{a^n},\ \left(\mbox{特に,}a^{-1}=\frac1a\right)\]
例
(1) $3^{-2}=\dfrac1{3^2}=\dfrac19$
(2) $(-2)^{-3}=\dfrac1{(-2)^3}=\dfrac1{-8}=-\dfrac18$
(3) $0.2^{-3}=\left(\dfrac15\right)^{-3}=\dfrac1{\left(\frac15\right)^3}=5^3=125$

1.2 整数の指数法則
これまで自然数であった指数を,整数にまで拡張したが,拡張したあとであってもこれまで成り立っていた指数法則はすべて成り立つ.(本当のところは指数法則が成り立つように,0や負の整数の指数を定義したのである.)
$a\neq0,\ b\neq0$ で,$m,\ n$ が整数のとき,\begin{align*} &[1]\ a^ma^n=a^{m+n}\\[5pt] &[2]\ (a^m)^n=a^{mn}\\[5pt] &[3]\ (ab)^n=a^nb^n\\[5pt] &[4]\ \frac{a^m}{a^n}=a^{m-n}\\[5pt] &[5]\ \left(\frac ab\right)^n=\frac{a^n}{b^n} \end{align*}
例
$[1]\ \ a^2a^{-3}=a^2\cdot\dfrac1{a^3}=\dfrac1a=a^{-1}=a^{2-3}$
$[2]\ \ (a^2)^{-3}=\dfrac1{(a^2)^3}=\dfrac1{a^6}=a^{-6}=a^{2\cdot(-3)}$
$[3]\ \ (ab)^{-2}=\dfrac1{(ab)^2}=\dfrac1{a^2b^2}=a^{-2}b^{-2}$

1.3 累乗根
$n$ を正の整数とするとき,$n$ 乗して $a$ になる数を
$a$ の $n$ 乗根
という.$a$ の $n$ 乗根は,方程式 $x^n=a$ の解である.
例
$9$ の2乗根(平方根ともいう)
$3$ と $-3$
$8$ の3乗根(立方根ともいう)
$x^3=8$ より $x^3-8=0$
$\therefore (x-2)(x^2+2x+4)=0$
よって,$2$ と $\ -1+\sqrt3i$ と $-1-\sqrt3i$
$-8$ の3乗根
$x^3=-8$ より $x^3+8=0$
$\therefore (x+2)(x^2-2x+4)=0$
よって,$-2$ と $\ 1+\sqrt3i$ と $1-\sqrt3i$
$16$ の4乗根
$x^4=16$ より $x^4-16=0$
$\therefore (x^2-4)(x^2+4)=0$
よって,$2$ と $-2$ と $2i$ と $-2i$
補足
① 2乗根,3乗根,4乗根,… をまとめて累乗根という.
② 一般に $a\neq0$ のとき,$a$ の $n$ 乗根は $n$ 個ある.
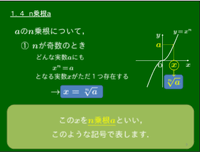
1.4 $n$ 乗根 $a$
前節で「$a$ の $n$ 乗根」というものを学んだが,これに似た用語に「$n$ 乗根 $a$」がある.これらは異なるものなので気を付けなければならない.
$a$ の $n$ 乗根について
- $\boldsymbol{n}$ が奇数のとき
どんな実数 $a$ にも $x^n=a$ となる実数 $x$ がただ1つだけ存在し,その $x$ を\[\sqrt[n]{a}\]と書き表し,「 $\boldsymbol{n}$ 乗根 $\boldsymbol{a}$ 」と読む.
例1 $8$ の3乗根は,$2$ と $-1\pm\sqrt3i$
よって,$2$ を $\sqrt[3]8$ と書き,
「3乗根8」
と読む:
$\sqrt[3]8=2$
例2 $-8$ の3乗根は,$-2$ と $1\pm\sqrt3i$
よって,$-2$ を $\sqrt[3]{-8}$ と書き,
「3乗根$-8$」
と読む:
$\sqrt[3]{-8}=-2$ - $\boldsymbol{n}$ が偶数のとき
(i) $a > 0$ のとき
$x^n=a$ となる $x$ が正負1個ずつある.その正の方を $\sqrt[n]a$ で表し,「 $\boldsymbol{n}$ 乗根 $\boldsymbol{a}$ 」と読む.そして負の方を $-\sqrt[n]a$ で表し,「 マイナス $\boldsymbol{n}$ 乗根 $\boldsymbol{a}$ 」と読む.
(ii) $a=0$ のとき
$\sqrt[n]0=0$
(iii) $a < 0$ のとき
$\sqrt[n]a$ は存在しない.
例 $16$ の4乗根は,
$2$ と $-2$ と $2i$ と $-2i$.
よって,
$2$ を $\sqrt[4]{16}$ と書き「4乗根16」と読む.
$-2$ を $-\sqrt[4]{16}$ と書き「マイナス4乗根16」と読む.
補足
$2$ 乗根 $a$ は,通常左上の $2$ を省略する:
\[\sqrt[2]a\ \to \ \sqrt a\]
また,「$2$ 乗根 $a$」や「平方根 $a$」とは呼ばず,「ルート $\boldsymbol{a}$」と呼ぶのが通例である.
重要な注意
$\boldsymbol{a>0}$ のとき,$\sqrt[n]a$ は,その定義から $n$ の偶奇にかかわらず正の数である:
この事実は,次節「1.5 累乗根の性質」で利用される.
1.5 累乗根の性質
平方根で成り立っていた以下の性質がそのまま一般の累乗根でも成り立つ.
$a>0, b>0$ で,$m,\ n,\ p$ が正の整数のとき,\begin{align*} &[1]\ \sqrt[n]a\,\sqrt[n]b=\sqrt[n]{ab\,}\\[5pt] &[2]\ \frac{\sqrt[n]a}{\sqrt[n]b}=\sqrt[n]{\frac ab}\\[5pt] &[3]\ (\sqrt[n]a)^m=\sqrt[n]{a^m}\\[5pt] &[4]\ \sqrt[m]{\sqrt[n]a}=\sqrt[mn]a\\[5pt] &[5]\ \sqrt[n]{a^m}=\sqrt[np]{a^{mp}} \end{align*}
証明の方針
$a > 0$ のとき,$\sqrt[n]a$ という数は,
正の数 $\cdots$ ①
であって,かつ
$\boldsymbol{(\sqrt[n]a)^n=a}$ $\cdots$ ②
を満たすただ1つの実数であることを利用.
証明
[1] $\sqrt[n]{\mathstrut{a}}>0,\ \sqrt[n]b>0$ より,$\sqrt[n]{\mathstrut{a}}\,\sqrt[n]b>0$.[①]
また,$(\sqrt[n]{\mathstrut{a}}\,\sqrt[n]b)^n=(\sqrt[n]{\mathstrut{a}})^n(\sqrt[n]b)^n=ab$.[②]
よって,$\sqrt[n]{\mathstrut{a}}\,\sqrt[n]b$ という数は,
正の数 [①]であって,
$n$ 乗すると $ab$ [②]になる実数
であるから,
$\sqrt[n]{\mathstrut a}\,\sqrt[n]b=\sqrt[n]{ab}$
[2] [1] と同様に示される.
[3] $\sqrt[n]a>0$ より,$(\sqrt[n]a)^m > 0$.[①]
また,$\{(\sqrt[n]a)^m\}^n=\{(\sqrt[n]a)^n\}^m=a^m$.[②]
よって,$(\sqrt[n]a)^m$ という数は,
正の数 [①]であって,
$n$ 乗すると $a^m$ [②]になる実数
であるから,
$(\sqrt[n]a)^m=\sqrt[n]{a^m}$
[4] $\sqrt[n]a>0$ より,$\sqrt[m]{\sqrt[n]a} > 0$.[①]
また,
$\left(\sqrt[m]{\sqrt[n]a}\right)^{mn}=\left\{\left(\sqrt[m]{\sqrt[n]a}\right)^m\right\}^n=\left(\sqrt[n]a\right)^n=a$.[②]
よって,$\sqrt[m]{\sqrt[n]a}$ という数は,
正の数 [①]であって,
$mn$ 乗すると $a$ [②]になる実数
であるから,
$\sqrt[m]{\sqrt[n]a}=\sqrt[mn\,]a$
[5] $a^m>0$ より,$\sqrt[n]{a^m} > 0$.[①]
また,
$\left(\sqrt[n]{a^m}\right)^{np}=\left\{\left(\sqrt[n]{a^m}\right)^n\right\}^p=\left(a^m\right)^p=a^{mp}$.[②]
よって,$\sqrt[n]{a^m}$ という数は,
正の数 [①]であって,
$np$ 乗すると $a^{mp}$ [②]になる実数
であるから,
$\sqrt[n]{a^m}=\sqrt[np\,]{a^{mp}}$
■
例
\[\begin{align*} \sqrt[3]4\,\sqrt[3]{54}&=\sqrt[3]4(\sqrt[3]2\sqrt[3]{27})\hspace{10mm}(\because [1])\\[5pt] &=\sqrt[3]8\,\sqrt[3]{27}\hspace{18mm}(\because [1])\\[5pt] &=2\cdot3\\[5pt] &=6 \end{align*}\]
\[\begin{align*} (\sqrt[8]9)^6&=\sqrt[8]{9^6}\hspace{22mm}(\because [3])\\[5pt] &=\sqrt[8]{(3^2)^6}\\[5pt] &=\sqrt[8]{3^{12}}\\[5pt] &=\sqrt[2\times4]{3^{3\times4}}\\[5pt] &=\sqrt[2]{3^{3}}\hspace{22mm}(\because [5])\\[5pt] &=(\sqrt3)^3\hspace{19mm}(\because [3])\\[5pt] &=3\sqrt3 \end{align*}\]

1.6 有理数の指数
ここでは指数を有理数にまで拡張することを考える.例えば正の数 $a$ に対して $a^{\frac23}$ や $a^{-\frac13}$ といったものがどんな数を表しているとするのがよいのだろうか.その指針となるのが指数法則である.指数が整数の場合の指数法則は次のようなものであった:
復習(整数の指数法則) $a\neq0$ で,$m,n$ が整数のとき, \[\begin{align*} &[1]\ \ a^ma^n=a^{m+n}\\[5pt] &[2]\ \ (a^m)^n=a^{mn} \end{align*}\]
いま $\boldsymbol a$ を正の数に制限して,これらの指数法則が,$m,n$ が有理数の場合でも成り立つと仮定してみる.例えば
\[\begin{align*} \left(a^{\frac23}\right)^3&=a^{\frac23\times3}\ \ \ (\mbox{整数の指数法則}[2])\\[5pt] &=a^2 \end{align*}\]
といった具合である.すると $a^{\frac23}$ という数は3乗すると $a^2$ になるから,$a^{\frac23}>0$ だとすれば3乗根 $a^2$ と考えられる:
\[a^{\frac23}=\sqrt[3]{a^2}\]
また,
\[\begin{align*} a^{\frac13}a^{-\frac13}&=a^{\frac13-\frac13}\ \ \ (\mbox{整数の指数法則}[1])\\[5pt] &=a^0=1\\[5pt] \therefore a^{\frac13}a^{-\frac13}&=1 \end{align*}\]
よって $a^{\frac13}$ が0でないとしてこの両辺を $a^{\frac13}$ で割ると, \[a^{-\frac13}=\frac1{a^{\frac13}}\]
以上のような考察から,有理数の指数を次のように定義する:
定義 $a>0$ で,$m,\ n$ が正の整数のとき, \begin{align*} & a^{\frac mn}=\sqrt[n]{a^m}\\[5pt] & a^{-\frac mn}=\frac1{a^{\frac mn}}=\frac1{\sqrt[n]{a^m}} \end{align*}
例
$5^{\frac34}=\sqrt[4]{5^3}$
$8^{\frac13}=\sqrt[3]8=2$
$9^{-\frac32}=\dfrac1{\sqrt{9^3}}=\dfrac1{(\sqrt9)^3}=\dfrac1{3^3}=\dfrac1{27}$

1.7 有理数の指数法則
指数を整数にまで拡張していた指数法則であるが,指数を有理数にまで拡張したあとでもそのまますべて成り立つ.
$a>0,\ b>0$ で,$r,\ s$ が有理数のとき,\begin{align*} &[1]\ a^ra^s=a^{r+s}\\[5pt] &[2]\ (a^r)^s=a^{rs}\\[5pt] &[3]\ (ab)^r=a^rb^r\\[5pt] &[4]\ \frac{a^r}{a^s}=a^{r-s}\\[5pt] &[5]\ \left(\frac ab\right)^r=\frac{a^r}{b^r} \end{align*}
例
$8^{\frac16}\times 8^{\frac32}=8^{\frac16+\frac32}=8^{\frac53}= \left\{\begin{array}{l} (2^3)^{\frac53}=2^5=32\\[5pt] \sqrt[3]{8^5}=(\sqrt[3]8)^5=2^5=32 \end{array}\right.$
$16^{-\frac12}= \left\{\begin{array}{l} (4^2)^{-\frac12}=4^{-1}=\dfrac14\\[5pt] \dfrac1{16^{\frac12}}=\dfrac1{\sqrt{16}}=\dfrac14 \end{array}\right.$
$a > 0$ のとき,
$\sqrt a\times\sqrt[6]a\div\sqrt[3]{a^2}=a^{\frac12}\times a^{\frac16}\div a^{\frac23}=a^{\frac12+\frac16-\frac23}=a^0=1$

1.8 無理数の指数
例 $2^{\sqrt2}\left(=2^{1.41421356\cdots}\right)$
$2^1,\ 2^{1.4},\ 2^{1.41},\ 2^{1.414},\ 2^{1.4142} \cdots$
という数の列は,小数部分を増やしていくと,どんどん一定の値に近付いていく.
その一定の値をもって,$2^{\sqrt2}$ とする.
補足
指数を無理数にまで拡張したので,$a > 0$ のとき,任意の実数 $x$ で $a^x$ の値が定められた.
1.2節で登場したすべての指数法則は,指数が実数になっても成り立つ.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [無料] | |
| 2. 指数関数 | [無料] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |