高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [無料] | |
| 2. 指数関数 | [無料] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |

2.指数関数
例えば銀行に1万円を預けたとしよう.これを元本という.現実とは相等に乖離している(※)が、数字を簡単にするため年利を10%としよう.そして数年間この1万円を預けっぱなしにしたとき,元利合計は一体いくらになるだろうか?
(※)2024年2月現在,とあるメガバンクの定期預金10年物の金利は 0.2%✨ となっている.
こういった利息計算をする場合,単利と複利という2つの計算方法がある.単利というのは毎年元本すなわち1万円に対して10%の利息が付くというもので,1年ごとに1000円ずつ増えていく計算になる.一方,複利というのは期末の利息が翌期の元本に加えられ,その合計額に対して翌期末に10%の利息が付くというもので,この計算方法では1年ごとに1.1倍になっていくことになる.銀行や郵便局の利息計算はこの複利という方法をとっている.
$x$ 年後の元利合計額を $y$ 円とする.$x$ と $y$ の関係は次のようになる.
1. 単利 $y=10000+1000x$
2. 複利 $y=10000\times1.1^x$
そしてこの2つのグラフは次のようになる.
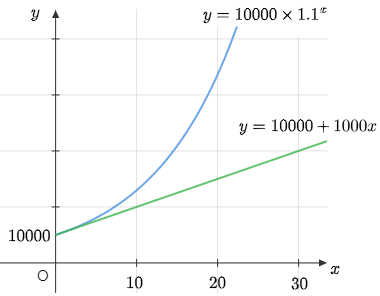
このグラフを見ると,単利計算の場合が直線的な変化であるのに対し,複利計算の場合は時間の経過と共に爆発的に増加していっていることがわかる.複利計算では $1.1^x$ のように $x$ が指数部分に現れているが,このような関数を指数関数という.ニュースなどで「指数関数的に増加している」といった表現を聞くことがあるが,それはこのグラフから見て取れるような急激な増加を意味する.
ここではこの指数関数について詳しく学習する.
2.1 指数関数
1.指数の拡張において,$a^x$ の $x$ を
自然数→整数→有理数→実数
へと拡張してきたが,「整数→有理数」へと拡張するとき,$a$ の値を正の数に制限をした.それは例えば $(-5)^{\frac12}$ という値がもはや実数とはならないからである.$a$ が正の数のときのみ,すべての実数 $x$ において $a^x$ がただ1つの実数として決まるのである.
$a>0$ のとき,任意の実数 $x$ に対して $a^x$ がただ1つ決まる.
これは $a^x$ が $x$ の関数であることを意味する.そこで,$a>0, a\neq1$ のとき,関数 $y=a^x$ を,$a$ を底(てい)とする指数関数 という.
指数関数 $a>0,\ a\neq1$ のとき, \[y=a^x\] を $\boldsymbol a$ を底とする指数関数 という.
補足
底の $a$ は1を除く正の数全体から選べるが,$a=1$ を除いたのは, $1^x$ が恒等的に1をとる関数であり,これから見ていくような指数関数としての性質を持ち合わせていないからである.

2.2 指数関数のグラフ
指数関数 $y=a^x$ のグラフがどのようになっているのか例を見てみよう.$x$ の値としていくつかの整数をとり, $a^x$ を計算した表を書き,それらの点をグラフに書き込んで滑らかに連結したのが下の図である.
例1 $y=2^x$
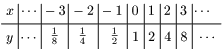
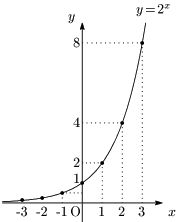
例2 $\displaystyle y=\left(\frac12\right)^x$
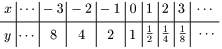
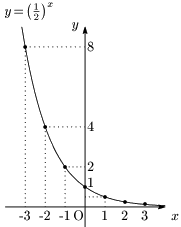
$y=2^x$ と $y=\left(\dfrac12\right)^x$ のグラフはよく似ているが,一方は右上がりのグラフで,他方は右下がりのグラフになっている.この違いはどこから来るかといえば,それは「底 $a$」である.この値が1より大きいか,0と1の間であるかによって,右上がりか右下がりが決まるのである.
$y=a^x$ のグラフ
指数関数 $y=a^x$ のグラフの特徴をまとめると次のようになる:
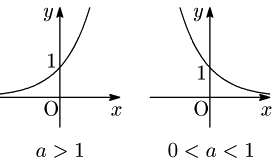
- $a>1$ のとき,右上がりの曲線
$0<a<1$ のとき,右下がりの曲線 - 点 $(0,1)$ を通る
- $x$ 軸が漸近線となる
「点 $(0,1)$ を通る」というのは任意の正の数 $a$ に対して $a^0=1$ となることからわかる.
漸近線とは,原点から遠いところにおいて限りなく近付く直線のことである.これは双曲線 $y=\dfrac 1x$ のところにも出てきた用語で,双曲線の場合は $x$ 軸と $y$ 軸が漸近線となるのであった.

2.3 指数関数の性質
指数関数 $y=a^x$ のグラフより,次のことがわかる:
指数関数の性質\begin{array}{cl} [1]&\mbox{定義域:実数全体}\\ &\mbox{値 域:正の実数全体}\\ [2]&a>1\mbox{のとき,単調に増加する}\\ & (p<q\iff a^p<a^q)\\ &0<a<1\mbox{のとき,単調に減少する}\\ & (p<q\iff a^p>a^q) \end{array}
補足
[2]により,
が成り立つ.(指数方程式で利用)
例題1 方程式 $2^{x+1}=8$ を解け.
こたえ
解答例を表示する例題2 不等式 $2^x<8$ を解け.
こたえ
解答例を表示する例題3 不等式$\displaystyle\left(\frac12\right)^x<\frac18$ を解け.
こたえ
解答例を表示する
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [無料] | |
| 2. 指数関数 | [無料] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |