高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | 問題 | |
| 1. 指数の拡張 | |||
| 2. 指数関数 | |||
| 3. 対数とその性質 | |||
| 4. 対数関数 | |||
| 5. 常用対数 |

1.指数の拡張
これまでに学んだのは
を意味しており,
自然数 → 整数 → 有理数 → 実数
へと拡張することを考える.まずは「自然数 → 整数」の拡張から始めよう.

1.1 0や負の整数の指数
50 や 3-2 は何を意味するのか
とするのが自然であろう.更に
と考えることができる.
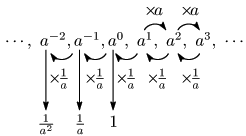
このように考えて,0や負の整数の指数を次のように定義する.
定義
例
(1)
(2)
(3)
(4)

1.2 整数の指数法則
拡張しても指数法則はすべて成り立つ
これまで自然数であった指数を,整数にまで拡張したが,拡張したあとであってもこれまで成り立っていた指数法則はすべて成り立つ.(本当のところは指数法則が成り立つように,0や負の整数の指数を定義したのである.)
例

1.3 累乗根
という.
例
よって,
よって,
よって,
よって,
補足
① 2乗根,3乗根,4乗根,… をまとめて累乗根(るいじょうこん)という.
② 複素数の範囲で考えると,一般に

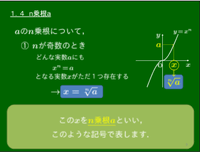
1.4
「
前節で「
1.
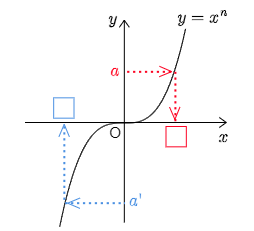
どんな
それに対応する□がただ1つ存在する.
このグラフを見ると,どんな実数
例1
よって,
「3乗根8」
と読む:
例2
よって,
「3乗根
と読む:
2.
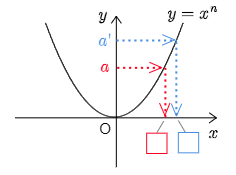
どんな非負の数
0以上の数□がただ1つ存在する.
このグラフをもとに,
(i)
(ii)
(iii)
例
よって,
よくある間違い
まとめ
- ただ1つの実数である
補足
また,「
重要な注意
この事実は,次節「1.5 累乗根の性質」で利用される.

1.5 累乗根の性質
ここでは