高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | |||
| 2. 複素数が表す図形 | |||
| 3. 極形式 | |||
| 4. ド・モアブルの定理 | |||
| 5. 複素数と図形 |

2. 複素数が表す図形
このノートでは特に断らない限り,$a+b\,i$ などと書けば,$a,\ b$ は実数であるとする.また,$z,\ \alpha,\ \beta,\ \gamma$ などの文字を断りなく複素数として記述することがある.
2.1 複素数の実数倍
複素平面上の点 $\alpha\ (=a+b\,i)$ に対して,実数倍 $t\,\alpha$ ($t$ は実数)は次のような点を表す:
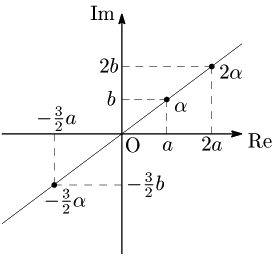
このことから一般に次が成り立つ.
定理 $\alpha\neq0$ のとき
複素平面上の3点 $0,\ \alpha,\ \beta$ が一直線上にある
$\iff \beta=k\alpha$ を満たす実数 $k$ が存在する
例題 3点 $0,\ 2+3\,i,\ 8+b\,i$ が一直線上にあるとき,$b$ の値を求めよ.
補足
$\alpha$ を$\overrightarrow{\alpha}$と思えば,平面ベクトルの場合と同じである.

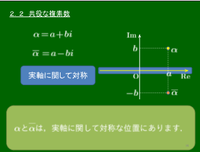
2.2 共役な複素数(complex conjugate 複素共役)
複素数 $\alpha=a+b\,i$ に対して,$a-b\,i$ を $\alpha$ の共役な複素数(共役複素数・複素共役complex conjugate)といい,$\overline{\alpha}$ で表す.
補足
$\alpha=a+b\,i$ のとき,$\overline{\alpha}=a-bi$ で,さらにこの共役は \[\overline{\overline{\alpha}}=\overline{a-b\,i}=a+b\,i\] 従って共役の共役は元の数である.
\[\overline{\overline{\alpha}}=\alpha\]

複素平面上の点 $\alpha$ に対して,実軸・虚軸・原点に関して対称移動した点がそれぞれどのように表されるかを実軸→原点→虚軸の順に見ていく.
- 実軸に関する対称移動
$\alpha=a+b\,i$ を実軸に関して対称移動した点は $a-b\,i$ となるから $\overline{\alpha}$ で表される. - 原点に関して対称移動
$\alpha=a+b\,i$ を原点に関して対称移動した点は $-a-b\,i(=-(a+b\,i))$ となるから $-\alpha$ で表される. - 虚軸に関する対称移動
$\alpha=a+b\,i$ を虚軸に関して対称移動した点は $-a+b\,i$ で,これは $\overline{\alpha}$ と原点に関して対称な点だから $-\overline{\alpha}$ で表される.