高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | 問題 | |
| 1. 指数の拡張 | |||
| 2. 指数関数 | |||
| 3. 対数とその性質 | |||
| 4. 対数関数 | |||
| 5. 常用対数 |

2.指数関数
例えば銀行に1万円を預けたとしよう.これを元本という.そして年利を10%としよう(※).この1万円を数年間にわたって預けっぱなしにしたとき,元利合計は一体いくらになるだろうか?
(※)2024年2月現在,とあるメガバンクの定期預金10年物の金利は 0.2%✨ となっている.現実とは相等に乖離しているが,数字を簡単にするために10%とした.
こういった計算をする場合,単利と複利という2つの計算方法がある.単利というのは毎年最初の元本すなわち1万円に対して10%の利息が付くというもので,1年ごとに1000円ずつ増えていく計算になる.一方,複利というのは期末の利息を引き出さずに翌期の元本に加えられ,その合計額に対して翌期末に10%の利息が付くというもので,この計算方法では1年ごとに1.1倍になっていくことになる.銀行や郵便局の利息計算はこの複利という方法をとっている.
$x$ 年後の元利合計額を $y$ 円とする.$x$ と $y$ の関係は次のようになる.
1. 単利 $y=10000+1000x$
2. 複利 $y=10000\times1.1^x$
そしてこの2つのグラフは次のようになる.
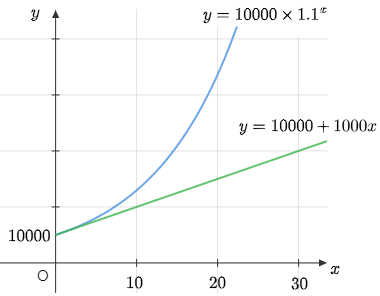
このグラフを見ると,単利計算の場合が直線的な変化であるのに対し,複利計算の場合は時間の経過と共に爆発的に増加していっていることがわかる.複利計算では $1.1^x$ のように $x$ が指数部分に現れているが,このような関数を指数関数という.ニュースなどで「指数関数的に増加している」といった表現を聞くことがあるが,それはこのグラフから見て取れるような急激な増加を意味する.
まずは問題
ここで,指数関数についての考察に入る前に,次の問いを考えてみたい.
Q. $\sqrt2$ と $\sqrt[3]4$ はどちらが大きいか?
$\sqrt2$ は「2乗すると2になる正の数」,$\sqrt[3]4$ は「3乗すると4になる正の数」である.$\sqrt2$ の方は古くから「一夜一夜に人見頃(ひとよひとよにひとみごろ)」という語呂合わせによって $1.41421356\cdots$ から概ね $1.41$ 程度であるとわかる.ところが $\sqrt[3]4$ の方はといえば,私たちの記憶のどこを探しても,即座に呼び出せる語呂もなければ,親しみやすい近似値も見当たらない.$1.4^3$ あるいは $1.5^3$ を逐一計算することの煩わしさが,かえってこの問いの輪郭を曖昧にする.このとき私たちは,単に $\sqrt2$ と $\sqrt[3]4$ という個別の2数の大小を判定するだけの安易な作業にとどまるのではなく,この問題の背後にある数学的な論理構造に目を向け,その観点から問いにアプローチすることで,より本質的な解決を目指したいのである.
突破口は有理数の指数にあり!
この問いに対する突破口は,私たちが既に身につけている有理数の指数という枠組みへと,問題自体を移し替えることにある.2つの数を有理数の指数として表記し直してみよう.
$\sqrt2=\sqrt[2]2=2^{\frac12}$
$\sqrt[3]4=\sqrt[3]{2^2}=2^{\frac23}$
このとき $\sqrt2$ と $\sqrt[3]4$ の比較は,$2^{\frac12}$ と $2^\frac23$ の比較へと姿を変える.
ここで「2」の部分は共通しているから,私たちの眼差しは,もはや指数部にのみ注がれることとなる.
$\dfrac12$ と $\dfrac23$ ――この2つの分数の間に横たわる大小関係,すなわち $\dfrac12<\dfrac23$ という事実は,果たして $2^{\frac12}<2^{\frac23}$ という不等式の成立を保証するのだろうか?
保証されるとすればその根拠はどこに求められるのか?
この問いこそが,指数関数という概念の本質へと私たちを導く端緒となる.いま,私たちは個別の数値の比較という安易な地平を離れ,指数関数の論理構造そのものへと静かに歩みを進めていくのである.
2.1 指数関数
前節の 1.指数の拡張
において,$a^x$ の $x$ を
自然数→整数→有理数→実数
へと拡張してきたが,「整数→有理数」へと拡張するとき,$a$ の値を正の数に制限をした.それは例えば $(-5)^{\frac12}$ という値がもはや実数とはならないからである.$a$ が正の数のときのみ,すべての実数 $x$ において $a^x$ がただ1つの実数として決まるのである.
$a>0$ のとき,任意の実数 $x$ に対して $a^x$ がただ1つ決まる.
これは $a^x$ が $x$ の関数であることを意味する.そこで,$a>0, a\neq1$ のとき,関数 $y=a^x$ を,$a$ を底(てい)とする指数関数 という.
指数関数とは $a>0,\ a\neq1$ のとき, \[y=a^x\] を $\boldsymbol a$ を底とする指数関数 という.
補足
底の $a$ は1を除く正の数全体から選べるが,$a=1$ を除いたのは, $1^x$ が恒等的に1をとる関数であり,これから見ていくような指数関数としての性質を持ち合わせていないからである.

2.2 指数関数のグラフ
指数関数 $y = a^x$ のグラフはどのような形状なのか――それを確かめるために,まずは幾つかの整数値を $x$ に与え,$a^x$ の値を計算してみることにしよう.
こうして得られた数値の列を表に記し,1つ1つの点として平面上に置いてみる.それらの点を,滑らかに結び合わせていくとき,指数関数のグラフが,徐々にその全容を現し始めるのである.
例1 $y=2^x$
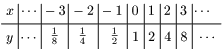

$x$ の値を $-3$ から $3$ まで $0.2$ 刻みでとり,
次々と点 $(x,\ 2^x)$ を打っていった様子.
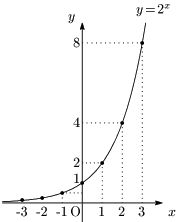
例2 $\displaystyle y=\left(\frac12\right)^x$