高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | 問題 | |
| 1. 指数の拡張 | |||
| 2. 指数関数 | |||
| 3. 対数とその性質 | |||
| 4. 対数関数 | |||
| 5. 常用対数 |

3.対数とその性質
3.1 対数とは
例えば,指数関数 $y=2^x$ を取り上げてみよう.関数とは $x$ の値に応じて $y$ の値がただ1つ定まる規則を指し示すものだが,こと指数関数のように,$x$ の増加とともに絶えず増大あるいは減少し続ける関数――すなわち単調性を有する関数においては,その特性ゆえに,$y$ の値をあらかじめ与えたとしても,そこに対応する $x$ の値がやはり唯一つに定まることとなる.実際にいくつかの具体例を計算してみれば,その事実は次のようになる:
$y=1$ のとき,$x=0$
$y=2$ のとき,$x=1$
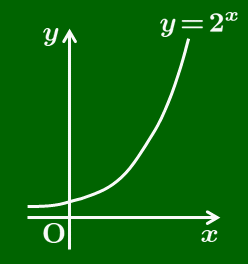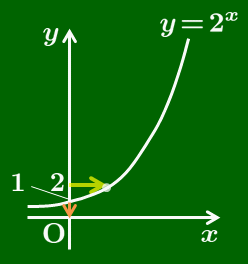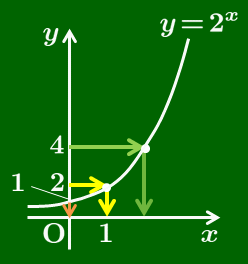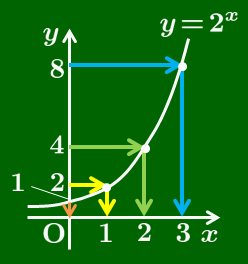
$y=4$ のとき,$x=2$
$y=8$ のとき,$x=3$
(スライドより抜粋)
そこで,「$y=M$ のとき,$M=2^x$ となる $x$ の値」を \[\log_2M\] で表す.

すると先に挙げた例はこの記号を用いて次のように表される:
\[\begin{align*}
\log_21&=0\\[5pt]
\log_22&=1\\[5pt]
\log_24&=2\\[5pt]
\log_28&=3
\end{align*}\]
となる.
$\log_aM$ を平たく言えば,
「$a$ を何乗すれば $M$ になるか」という数
であると表現することができる.先に挙げた例で言えば
$\log_21$ は2を何乗すると1になるかという数→0 ($2^0=1$)
$\log_22$ は2を何乗すると2になるかという数→1 ($2^1=2$)
$\log_24$ は2を何乗すると4になるかという数→2 ($2^2=4$)
$\log_28$ は2を何乗すると8になるかという数→3 ($2^3=8$)
となる.
一般に, $a>0,a\neq1,M>0$ のとき,$a^p=M$ を満たす実数 $p$ がただ1つ存在し,これを \[\log_aM\] と書き,$\boldsymbol{a}$ を底(てい)とする $\boldsymbol{M}$ の対数という.また,$M$ を真数という.
対数 $a>0,\ a\neq1,\ M>0$ のとき,\[a^p=M \iff p=\log_aM \]


