高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | 問題 | |
| 1. 指数の拡張 | |||
| 2. 指数関数 | |||
| 3. 対数とその性質 | |||
| 4. 対数関数 | |||
| 5. 常用対数 |

4.対数関数
4.1 対数関数
$a$ が底の条件,すなわち正であって1でない数であるとき,$y=a^x$ は $x$ の値が1つ決まればそれに応じて $y$ の値がただ1つ決まった.つまり $y$ は $x$ の関数である.
ここで注目すべきは,この対応が単なる一方向的な関数関係にとどまるものではなく,$x$ と $y$ との間に厳密な1対1の対応が成立している,という事実にほかならない.
$y=a^x$ の $x$ と $y$ は1対1対応
故に,今度は $y$ の値を先に与えたとしても,その値に対応する $x$ の値は,やはりただ1つに定まることとなる.すなわち「$x$ は」 $y$ の関数である,と言い換えることもできよう.
このように,逆の対応までもが関数として成立するのは,ひとえに指数関数の単調性という性質によるものである.
例 $y=2^x$
$x=0$ のとき $y=1$.逆に $y=1$ のとき $x=0$.
$x=1$ のとき $y=2$.逆に $y=2$ となる $x=1$.
$x=2$ のとき $y=4$.逆に $y=4$ となる $x=2$.
$\vdots$
任意の正の実数 $y$ に対して,$y=a^x$ を満たす $x$ を $\log_ay$ と書き表した.つまり $x=\log_ay$ である.しかし,数学の慣習においては,先に定める記号を $x$ とし,それに応じて決定される値を $y$ とするのが常である.そのため,
\[y=\log_ax\]
という表記が,ここでも用いられることになるのである.
対数関数 $a > 0,a\neq1$ のとき,
\[y=\log_a x\]
を,$\boldsymbol{a}$ を底(てい)とする $\boldsymbol{x}$ の対数関数という.

4.2 対数関数のグラフ
対数関数 $y=\log_a x$ のグラフは,いかなる姿を描くのだろうか.まずは,対数の値が比較的明瞭に定まるいくつかの $x$ の値について,その対応する値を表にまとめてみることにしよう.そののち,得られた $(x,\ y)$ の組を座標平面上に1つ1つ記し,それらを滑らかに結んでいくことで,対数関数の軌跡が次第にその輪郭を現してくるはずである.
例1 $y=\log_2x$
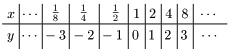
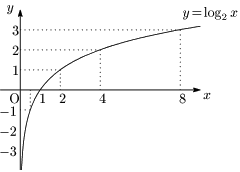

点$(x,\ \log_2x)$ を,$x$ の値を $0.2$ から $3$ まで
$0.2$ 刻みで増加させたときの変化の様子
例2 $y=\log_{\frac12}x$
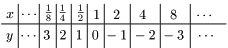
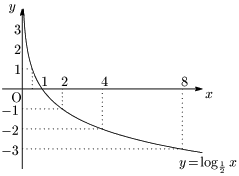
底が,$2$ と $\dfrac12$ の2つだけを調べたが,共通点と相違点は何であろうか.
グラフの共通点と相違点
上の2つのグラフについて,共通点4つと相違点1つを確認しておく.