高校数学[総目次]
数学B 第3章 統計的な推測
| スライド | ノート | |
| 1. 確率変数と確率分布 | ||
| 2. 確率変数の期待値と分散 | ||
| 3. 確率変数の変換 | ||
| 4. 確率変数の和と期待値 | ||
| 5. 独立な確率変数と期待値・分散 | ||
| 6. 二項分布 | ||
| 7. 正規分布 | ||
| 8. 母集団と標本 | ||
| 9. 推定 | ||
| 10. 仮説検定 |

6.二項分布
6.1 二項分布とは
さいころを3回投げたとき,2以下の目がでる回数を $X$ とすると, $X$ は確率変数である.1回の試行において2以下の目が出る確率は $\dfrac26=\dfrac13$,2以下の目が出ない(3以上の目が出る)確率は $1-\dfrac13=\dfrac23$ であるから,$X$ の分布は次のように計算される:
\[\begin{align*} P(X=0)&=\ {_3\rm C_0}\ \left(\frac23\right)^3\ =\ \frac8{3^3}\\[5pt] P(X=1)&={_3\rm C_1}\frac13\cdot\left(\frac23\right)^2=\frac{12}{3^3}\\[5pt] P(X=2)&={_3\rm C_2}\left(\frac13\right)^2\cdot\frac23=\frac6{3^3}\\[5pt] P(X=3)&=\ {_3\rm C_3}\ \left(\frac13\right)^3\ =\ \frac1{3^3}\\[5pt] \end{align*}\]
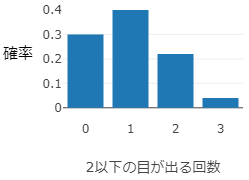
$X$ が従う分布
この例のように,$n$ 回の反復試行で事象Aが起こる回数を表す確率変数 $X$ が従う分布は,次に説明するように二項分布と呼ばれている.

1回の試行で事象 $A$ の起こる確率が $p$ とする.このとき事象 $A$ が起こらない確率を $q$ とすると, $q=1-p$ である.
この試行を $n$ 回繰り返したとき,事象 $A$ の起こる回数を $X$ とすると,$X$ は確率変数となり,
\[P(X=r)={_n{\rm C}}_r\ p^rq^{n-r}\]
である.従って確率変数 $X$ の分布は次のようになる.
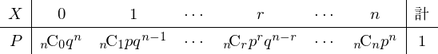
この確率変数 $X$ が従う分布を二項分布(binomial distribution)といい,$B(n,p)$ で表す.
二項分布 1回において事象Aが起こる確率が $p$ である試行を $n$ 回繰り返したとき,事象Aが起こる回数を $X$ とすると,$X$ は確率変数となり,二項分布 $B(n,p)$ に従う.
「二項」という用語は二項定理
\[(a+b)^n={_n\rm C}_0\,a^n\!+\!{_n\rm C}_1\,a^{n-1}b\!+\!{_n\rm C}_2\,a^{n-2}b^2\!+\!\cdots\!+\!{_n\rm C}_n\,b^n\]
からきており,この展開項において $a$ を $q$ に,$b$ を $p$ に置き換えると,上の表の確率が現れる.また左辺は
\[(a+b)^n=(q+p)^n=1^n=1\]
であるから,確かに確率の合計は1である.
例1 さいころを5回投げるとき,1の目が出る回数を $X$ とすると,$X$ は二項分布 $B\left(5,\dfrac16\right)$ に従う確率変数である.
例2 硬貨を3回投げるとき,表の面が出る回数を $X$ とすると,$X$ は二項分布 $B\left(3,\dfrac12\right)$ に従う確率変数である.

6.2 二項分布の期待値と分散
ある試行で事象 $A$ の起こる確率が $p$ であるとし,この試行を $n$ 回繰り返す.$k$ 回目の試行で $A$ が起これば 1,起こらなければ 0 をとる確率変数を $X_k$ とすると,$X_k$ の従う分布は次のようになる.
| $X_k$ | 0 | 1 | 計 |
| $P$ | $1-p$ | $p$ | $1$ |
故に $X_k$ の期待値 $E(X_k)$ は
\[E(X_k)=0\cdot(1-p)+1\cdot p=p\]
である.ここで $X$ を
\[X=X_1+X_2+\cdots+X_n\]
とすると, $X$ はこの試行を $n$ 回繰り返したとき,事象 $A$ が起こる回数を表す確率変数となる.
$X$ の期待値 $E(X)$ は
\[\begin{align*} E(X)&=E(X_1+X_2+\cdots+X_n)\\[5pt] &=E(X_1)+E(X_2)+\cdots+E(X_n)\\[5pt] &=p+p+\cdots+p\\[5pt] &=np \end{align*}\]
また,
\[E({X_k}^2)=0^2\cdot (1-p)+1^2\cdot p=p\]
であるから,$X_k$ の分散 $V(X_k)$ は
\[\begin{align*} V(X_k)&=E({X_k}^2)-\{E(X_k)\}^2\\[5pt] &=p-p^2\\[5pt] &=p(1-p) \end{align*}\]
となり,反復試行では各回の試行は独立であるから,確率変数 $X_1,X_2,\cdots,X_n$ も独立で,
\[\begin{align*} V(X)&=V(X_1+X_2+\cdots+X_n)\\[5pt] &=V(X_1)+V(X_2)+\cdots+V(X_n)\\[5pt] &=np(1-p) \end{align*}\]
が成り立つ.(独立な確率変数の和の分散)
まとめ 確率変数 $X$ が二項分布 $B(n,p)$ に従うとき, \[\begin{align*} &E(X)=np\\[5pt] &V(X)=np(1-p)\\[5pt] &\sigma(X)=\sqrt{np(1-p)} \end{align*}\]
例題 さいころを50回投げて,2以下の目が出た回数を $X$ とするとき,$E(X), V(X)$ を求めよ.
答
確率変数 $X$ は,二項分布 $B\left(50,\dfrac 13\right)$ に従うから,
\[\begin{align*} E(X)&=50\cdot\frac13=\frac{50}3\\[5pt] V(X)&=50\cdot\frac13\left(1-\frac13\right)=\frac{100}9 \end{align*}\]

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第3章 確率分布と統計的な推測
| スライド | ノート | |
| 1. 確率変数と確率分布 | ||
| 2. 確率変数の期待値と分散 | ||
| 3. 確率変数の変換 | ||
| 4. 確率変数の和と期待値 | ||
| 5. 独立な確率変数と期待値・分散 | ||
| 6. 二項分布 | ||
| 7. 正規分布 | ||
| 8. 母集団と標本 | ||
| 9. 推定 | ||
| 10. 仮説検定 |
