高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | ||
| 2. 2次方程式の解と判別式 | ||
| 3. 解と係数の関係 | ||
| 4. 剰余の定理・因数定理 | ||
| 5. 高次方程式 |

1.複素数
このノートでは,複素数 a+bi について,「 a, b は実数」という断りを省略することがある.
1.1 複素数
方程式 x2=a は,a≧0 のとき x=±√a を解にもつ.例えば x2=1 のとき x=±1,x2=25 のとき x=±5,x2=0 のとき x=0 等々.一方,x2=−1 や x2=−4 は解をもたない.どんな数も2乗すると0以上になるからだ.
ここでの目標は,方程式 x2=a において,a<0 の場合であっても解をもつように数を拡張することにある.
2乗すると負になる数を考える
方程式「x2=(負の数)」にも解をもたせるためにはこれまでの数だけでは足りない.次に示す全く新しい数「 i 」を考えることで,この難局を乗り越える.
虚数単位
2乗すると −1 になる数を i で表す:
i2=−1
この i を虚数単位(きょすうたんい,imaginay unit)という.imaginary unit は直訳すれば「想像上の単位」ということになろうが,歴史上の数学者が編み出したこの i は,遊び心といったおふざけなどで終始することのない大発明なのである.i が数学の世界に登場したことで,数学は大いなる進歩を遂げることになる.残念なことに,その素晴らしい内容の大部分は大学で学ぶこととなる.

この虚数単位 i を用いてここに「複素数(ふくそすう)」と呼ばれる新しい数を導入する:
複素数
実数 a,b を用いて,a+bi と表される数を複素数 (complex number)という:
複素数
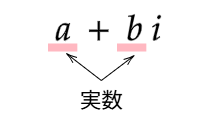
このとき,a を実部(じつぶ),b を虚部(きょぶ)という.もう少し簡単な表現にすると
(実数)+(実数) i
の形をしている数を複素数というのである.具体的には 2+3i や −4+√5i や −√23−√78i などである.こういった数の総称が複素数である.
いくつかの重要な補足
複素数 a+bi は実数をも内包する新しい数
① b=0 のとき,a+bi は a とする.
つまり実数も複素数である.例えば5は 5+0i,−2 は −2+0i など.
② b≠0 のとき,a+bi を虚数という.
特に,a=0 のときは,a+bi を bi と表し,これを純虚数という.
例えば 2i や −3i, √62i など.
③ 以上により,次のような包含関係になる:
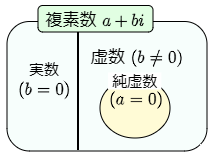
要するに,私たちが知っている数はすべて複素数であるということである.
2つの複素数が等しいとはどういうときをいうのか
2つの複素数 a+bi と c+di が等しいとは,実部,虚部がそれぞれ等しいときをいう:
複素数の相等 a+bi=c+di⟺a=c, b=d
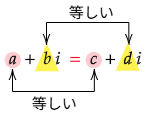
特に,0 は 0+0i であるから
a+bi=0⟺a=b=0
である.
読むとかえって混乱するかもしれない補足
上の2つの囲み書きを見ると,そんなことは当たり前ではないかと思われるかもしれない.恐らく複素数が a+bi という見慣れた表情をしているせいであろうが,虚数単位 i という不思議なものを使って数学者が作り出した完全に新しい数である.この数がどういう性質を持っているものなのかを,私たちは知識0の状態から学ばなくてはならない.
イメージとして例を出すと a|b と書いて「ひまわり数」と呼ぶ新しい数が作られたとしよう.そして2つのひまわり数 a|b と c|d が等しいことを a+2b=c+2d が成り立つときと約束して,1|2=3|1 などの関係が成り立つと考えたらどうだろう.実際にはひまわり数は存在しないが,新しい数を作ったら,その数に対する約束事・ルールを1つ1つ決めていかなければならないのである.

共役な複素数とは
a+bi と a−bi を互いに共役な複素数(きょうやくなふくそすう),または複素共役 (complex conjugate)という.「互いに」というのは,例えば 2+3i と共役な複素数は 2−3i であり,逆に 2−3i と共役な複素数は 2+3i である.
実数 a を a=a+0i と思えば,a+0i と共役な複素数は a=a−0i すなわち a であるから,結局 実数 a と共役な複素数は a 自身である.

1.2 複素数の四則計算
複素数という新しい数についての四則計算を次のように取り決める:
複素数の四則計算の定義 a,b,c,d を実数とする.2つの複素数a+bi, c+di について,加法 (a+bi)+(c+di)=(a+c)+(b+d)i減法 (a+bi)−(c+di)=(a−c)+(b−d)i乗法 (a+bi)(c+di)=(ac−bd)+(ad+bc)i除法 c+dia+bi=ac+bda2+b2+ad−bca2+b2i ※ただし,除法ではa+bi≠0.
複素数の四則計算は,虚数単位 i を i2=−1 とする以外は,i も a や b などの他の文字と同様に通常の文字式と同じ取り扱いで計算できる:
加法:(1+2i)+(3−4i)=(1+3)+(2−4)i
=4−2i
減法:(1+2i)−(3−4i)=(1−3)+{2−(−4)}i
=−2+6i
乗法:(1+2i)(3−4i)=1⋅3−1⋅4i+2i⋅3−2i⋅4i
=3−4i+6i+8
=11+2i
特に,
(1+2i)(1−2i)=12−(2i)2
=1+4
=5 (実数)
除法:1+2i3−4i=(1+2i)(3+4i)(3−4i)(3+4i)
=1⋅3+1⋅4i+2i⋅3+2i⋅4i32+42
=−5+10i25
=−15+25i
(次の事実は基本的だが証明を要する.)
定理 α, β を複素数とするとき,αβ=0⟺α=0 または β=0
重要な注意
虚数に大小や正負の概念はない
虚数については,
① 大小関係 ② 正負
を考えない.
例えば,次のような表現はいずれも誤りである:
1+2i<3+4i 1+2i>0

1.3 負の数の平方根
2乗(平方)して a になる数を a の平方根と呼んだ.例えば9の平方根は 3 と −3 であり,5 の平方根は √5 と −√5 である.どんな正の数 a にも平方根は2つあり,それを √a と −√a と表すのであった.先の例ではそれぞれ ±√9,±√5 であり,「±」の記号を用いてまとめて表現されることが多い.このことを方程式で表すと,非負の数 a の平方根を x として
x2=a ∴x=±√a
となる.
ところで実数はどんな数でも2乗すると0以上の数になるのだから,負の数の平方根は存在しなかった.従って例えば方程式 x2=−5 の解を x=±√−5 と書いたところでそんな数は存在せず,「解なし」と書くしかなかった.しかし虚数単位 i を導入したことで,これからは負の数の平方根も考えられるようになったのである.
Q. −5 の平方根は?
A.
−5 の平方根を x とすると, x2=−5x2+5=0x2−(√5i)2=0 (←(√5i)2=−5)(x+√5i)(x−√5i)=0 (←A2−B2=(A+B)(A−B))∴x=±√5i 従って,−5 の平方根は,√5i と−√5i.
このようにして,方程式 x2=−5 の解が ±√5i となることがわかった.だとしたら,例えば x2=5 の解を x=±√5 と表現してきたように,x2=−5 の解も x=±√−5 と表現できたなら一貫性があってよい.そこで √−5 と書いたらそれは √5i という複素数を意味するものとして定めよう:
√−5 は √5i を意味する,つまり
√−5=√5i
すると,−5 の平方根は,±√−5 と表現できて,これは ±√5i を意味するのである.
一般に,a>0 のとき,√−a は √ai を意味するものと定める:
√−a の意味 a>0 のとき, √−a=√ai 特に, √−1=i
例
√−6=√6i
√−12=√12i=2√3i
√−2√−3=√2i√3i=√6i2=−√6
3√−2=3√2i=3√2i√2i×√2i=3√2i−4=−3√24i
負の数の平方根
a>0 のとき,−a の平方根は,
±√−a すなわち ±√ai
例
−4 の平方根は,±2i
−7 の平方根は,±√7i
以上により,負の数も含めた任意の実数 a について,その平方根を表すことができるようになった.

注意
1=−1 ???
次のような計算は誤りである:
√−2√−3=√(−2)×(−3)=√6 (←誤り)
√(a√(b=√(ab の公式は,a,b がともに正の数で成り立つもので,負の数では成り立たない.
次は 1 と −1 が等しくなるというよく知られた不思議な式である.(もちろん正しくない.)

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | ||
| 2. 2次方程式の解と判別式 | ||
| 3. 解と係数の関係 | ||
| 4. 剰余の定理・因数定理 | ||
| 5. 高次方程式 |

