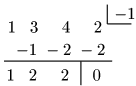高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | [無料] | |
| 2. 2次方程式の解と判別式 | [無料] | |
| 3. 解と係数の関係 | [会員] | |
| 4. 剰余の定理・因数定理 | [会員] | |
| 5. 高次方程式 | [会員] |

5.高次方程式
5.1 高次方程式の解法
多項式 $P(x)$ が3次以上のとき,方程式 $P(x)=0$ を高次方程式という.
解法の手順
- 発見的に1つ解 ($\alpha$ とする) を見つける.
- $P(x)$ を $x-\alpha$ で割る.
- 商が2次式になるまで①,②を繰り返す.
例題 $x^3+3x^2+4x+2=0$ を解け.
手順① 発見的に解の1つを見つける
係数が整数,かつ最高次の係数が1
→ 解の候補は定数項の正負の約数(前節)
→ $\pm1,\ \pm2$ このうち $-1$ が解.


手順③ 手順①,②を全ての因数が2次以下になるまで繰り返す.
よって,$(x+1)(x^2+2x+2)=0$ より
\[\underline{\boldsymbol{x=-1,\ -1\pm i}}\]

5.2 3次方程式の解と係数の関係
3次方程式 $ax^3+bx^2+cx+d=0$ の3つの解を,$\alpha,\beta,\gamma$ とすると, \[ax^3+bx^2+cx+d=a(x-\alpha)(x-\beta)(x-\gamma)\] と因数分解できる.このとき \[\begin{align*} (\mbox{右辺})&=a\{x^3\!-\!(\alpha+\beta+\gamma)x^2\!+\!(\alpha\beta+\beta\gamma+\gamma\alpha)x\!-\!\alpha\beta\gamma\}\\[5pt] &=ax^3\!-\!a(\alpha+\beta+\gamma)x^2\!+\!a(\alpha\beta+\beta\gamma+\gamma\alpha)x\!-\!a\alpha\beta\gamma \end{align*}\] となるから,2次以下の係数を比較して, \[\begin{align*} b&=-a(\alpha+\beta+\gamma)\\[5pt] c&=a(\alpha\beta+\beta\gamma+\gamma\alpha)\\[5pt] d&=-a\,\alpha\beta\gamma \end{align*}\] よって,次を得る:
3次方程式の解と係数の関係 3次方程式 $ax^3\!+\!bx^2\!+\!cx\!+\!d\!=\!0$ の3つの解を $\alpha,\beta,\gamma$ とすると,\begin{align*}&\alpha+\beta+\gamma=-\frac ba\\ &\alpha\beta+\beta\gamma+\gamma\alpha=\frac ca\\ &\alpha\beta\gamma=-\frac da\end{align*}
補足
\[ax^3+bx^2+cx+d=a(x-\alpha)(x-\beta)(x-\gamma)\] という式は,因数定理から示される:
$P(x)=ax^3+bx^2+cx+d$ とおくと,$P(\alpha)=0$,$P(\beta)=0$,$P(\gamma)=0$ であるから,$P(x)$ は $(x-\alpha)(x-\beta)(x-\gamma)$ を因数にもつ.よって $k$ を定数として, \[P(x)=k(x-\alpha)(x-\beta)(x-\gamma)\] となる.これは $x$ の恒等式であるから,$k=a$.
例題 3次方程式 $x^3\!+\!ax^2\!+\!x\!+\!b\!=\!0$ の解のうち,2つが $-1$ と 2 のとき,定数 $a,b$ の値を求めよ.
答
解答例を表示する >
補足
「解と係数の関係」という用語を持ち出さず,恒等式の考え方を用いた次のような解法も重要:
~・~・~・
$-1$ と $2$ 以外の解を $p$ とすると,
\[x^3+ax^2+x+b=(x+1)(x-2)(x-p)\]
と因数分解できる.右辺を展開して1次の係数を比較すると,
\[1=-2+2p-p\ \ \ \therefore p=3\]
よって,$(x+1)(x-2)(x-3)$ を展開して係数を比較することで,$\underline{\boldsymbol{a=-4,\ b=6}}$ を得る.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | [無料] | |
| 2. 2次方程式の解と判別式 | [無料] | |
| 3. 解と係数の関係 | [会員] | |
| 4. 剰余の定理・因数定理 | [会員] | |
| 5. 高次方程式 | [会員] |