高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | [無料] | |
| 2. 2次方程式の解と判別式 | [無料] | |
| 3. 解と係数の関係 | [会員] | |
| 4. 剰余の定理・因数定理 | [会員] | |
| 5. 高次方程式 | [会員] |

1.複素数
このノートでは,複素数 $a+b\,i$ について,「 $a,\ b$ は実数」という断りを省略することがある.
1.1 複素数
方程式 $x^2=a$ は,$a\geqq0$ のとき $x=\pm\sqrt a$ を解にもつ.例えば $x^2=1$ のとき $x=\pm1$,$x^2=25$ のとき $x=\pm5$,$x^2=0$ のとき $x=0$ 等々.一方,$x^2=-1$ や $x^2=-4$ は解をもたない.どんな数も2乗すると0以上になるからだ.
ここでの目標は,方程式 $x^2=a$ において,$a<0$ の場合であっても解をもつように数を拡張することにある.
虚数単位
2乗すると $-1$ になる数を $i$ で表す:
$i^2=-1$
この $i$ を虚数単位($\,i\,\rm{maginay\ unit}$)という.
この虚数単位 $i$ を用いてここに「複素数」と呼ばれる新しい数を導入する:
複素数
実数 $a, b$ を用いて,$a+b\,i$ と表される数を複素数 (complex number)という:
$a+b\,i$ ($a,b$ は実数)
このとき,$a$ を実部,$b$ を虚部という.もう少し簡単な表現にすると
(実数)+(実数)× $i$
の形をしている数を複素数というのである.具体的には $2+3\,i$ や $-4+\sqrt5\,i$ や $-\dfrac{\sqrt2}3-\dfrac{\sqrt7}8\,i$ などである.こういった数の総称が複素数である.
補足
① $b=0$ のとき,$a+b\,i$ は $a$ とする.
つまり,実数も複素数である.
② $b\neq0$ のとき,$a+b\,i$ を虚数という.
特に,$a=0$ のときは,$a+b\,i$ を $b\,i$ と表し,これを純虚数という.
例えば $2\,i$ や $-3\,i,\ \dfrac{\sqrt6}2i$ など.
③ 以上により,次のような包含関係になる:
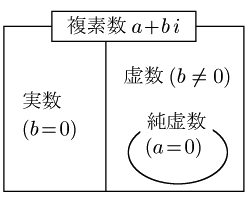
複素数の相等
2つの複素数 $a+b\,i$ と $c+d\,i$ が等しいとは,実部,虚部がそれぞれ等しいときをいう:
特に,
共役な複素数
$a+b\,i$ と $a-b\,i$ を互いに共役な複素数,または複素共役 (complex conjugate)という.
実数 $a$ を $a=a+0\,i$ と思えば,$a+0\,i$ と共役な複素数は $a=a-0\,i$ すなわち $a$ であるから,結局実数 $a$ と共役な複素数は $a$ 自身である.

1.2 複素数の四則計算
複素数という新しい数についての四則計算を次のように取り決める:
複素数の四則計算の定義 $a,b,c,d$ を実数とする.2つの複素数$a+bi,\ c+di$ について,\[\begin{align*} &\mbox{加法}\ \ (a\!+\!bi)\!+\!(c\!+\!di)\!=\!(a\!+\!c)\!+\!(b\!+\!d)i\\[5pt] &\mbox{減法}\ \ (a\!+\!bi)\!-\!(c\!+\!di)\!=\!(a\!-\!c)\!+\!(b\!-\!d)i\\[5pt] &\mbox{乗法}\ \ (a\!+\!bi)(c\!+\!di)\!=\!(ac\!-\!bd)\!+\!(ad\!+\!bc)i\\[5pt] &\mbox{除法}\ \ \ \frac{c\!+\!di}{a\!+\!bi}\!=\!\frac{ac\!+\!bd}{a^2\!+\!b^2}\!+\!\frac{ad\!-\!bc}{a^2\!+\!b^2}i \end{align*}\] ※ただし,除法では$a\!+\!b\,i\!\neq\!0.$
複素数の四則計算は,虚数単位 $i$ を $i^2=-1$ とする以外は,$i$ も $a$ や $b$ などの他の文字と同様に通常の文字式と同じ取り扱いで計算できる:
加法:$(1+2\,i)+(3-4\,i)=(1+3)+(2-4)\,i$
$=4-2\,i$
減法:$(1+2\,i)-(3-4\,i)=(1-3)+\{2-(-4)\}\,i$
$=-2+6\,i$
乗法:$(1+2\,i)(3-4\,i)=1\cdot3-1\cdot4\,i+2\,i\cdot3-2\,i\cdot4\,i$
$=3-4\,i+6\,i+8$
$=11+2\,i$
特に,
$(1+2\,i)(1-2\,i)=1^2-(2\,i)^2$
$=1+4$
$=5$ (実数)
除法:$\dfrac{1+2\,i}{3-4\,i}=\dfrac{(1+2\,i)(3+4\,i)}{(3-4\,i)(3+4\,i)}$
$=\dfrac{1\cdot3+1\cdot4\,i+2\,i\cdot3+2i\cdot4\,i}{3^2+4^2}$
$=\dfrac{-5+10\,i}{25}$
$=-\dfrac15+\dfrac25\,i$
(次の事実は基本的だが証明を要する.)
定理 $\alpha,\ \beta$ を複素数とするとき,\[\alpha\beta=0\iff\alpha=0\ \mbox{または}\ \beta=0\]
重要な注意
虚数については,
① 大小関係 ② 正負
を考えない.
例えば,次のような表現はいずれも誤りである:
\[1+2\,i < 3+4\,i\] \[1+2\,i > 0\]

1.3 負の数の平方根
Q. $-5$ の平方根は?
A.
$-5$ の平方根を $x$ とすると, \[\begin{align*} x^2&=-5\\[5pt] x^2+5&=0\\[5pt] x^2-(\sqrt5\,i)^2&=0\ \ \ (\gets(\sqrt5\,i)^2=-5)\\[5pt] (x+\sqrt5\,i)(x-\sqrt5\,i)&=0\ \ \ (\gets A^2\!-\!B^2\!=\!(A\!+\!B)(A\!-\!B))\\[5pt] \therefore x&=\pm\sqrt5\,i \end{align*}\] 従って,$-5$ の平方根は,$\sqrt5\,i$ と$-\sqrt5\,i$.
ここで,$\sqrt{-5}$ を $\sqrt5\,i$ と意味するものと定める:
\[\sqrt{-5}=\sqrt5\,i\]
すると,$-5$ の平方根は,$\pm\sqrt{-5}$ と表せて,これは $\pm\sqrt5\,i$ を意味する.
一般に,$a>0$ のとき,$\sqrt{-a}$ は $\sqrt a\,i$ を意味するものと定める:
$\sqrt{-a}$ の意味 $a > 0$ のとき, \[\sqrt{-a}=\sqrt a\,i\] 特に, \[\sqrt{-1}=i\]
例
$\sqrt{-6}=\sqrt6\,i$
$\sqrt{-12}=\sqrt{12}\,i=2\sqrt3\,i$
$\sqrt{-2}\sqrt{-3}=\sqrt2\,i\sqrt3\,i=\sqrt6\,i^2=-\sqrt6$
$\dfrac3{\sqrt{-2}}=\dfrac3{\sqrt2\,i}=\dfrac{3\sqrt2\,i}{\sqrt2\,i\times\sqrt2\,i}=\dfrac{3\sqrt2\,i}{-4}=-\dfrac{3\sqrt2}4\,i$
注意
上の3番目の例で,次のような計算は誤りである:
$\sqrt{-2}\sqrt{-3}=\sqrt{(-2)\times(-3)}=\sqrt6$ (←誤り)
$\sqrt a\sqrt b=\sqrt{ab}$ の公式は,$a ,b$ がともに正の数で成り立つもので,負の数では成り立たない.
負の数の平方根
$a>0$ のとき,$-a$ の平方根は,
$\pm\sqrt{-a}$ すなわち $\pm\sqrt a\,i$
例
$-4$ の平方根は,$\pm2\,i$
$-7$ の平方根は,$\pm\sqrt7\,i$
以上により,負の数も含めた任意の実数 $a$ について,その平方根を表すことができるようになった.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | [無料] | |
| 2. 2次方程式の解と判別式 | [無料] | |
| 3. 解と係数の関係 | [会員] | |
| 4. 剰余の定理・因数定理 | [会員] | |
| 5. 高次方程式 | [会員] |

