高校数学[総目次]
数学C 第2章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | |||
| 2. 複素数が表す図形 | |||
| 3. 極形式 | |||
| 4. ド・モアブルの定理 | |||
| 5. 複素数と図形 |

演習問題
問題1【発展】
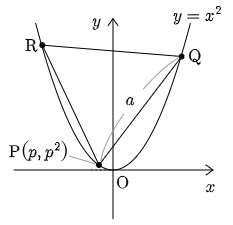
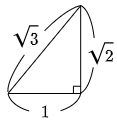
△PQRは一辺の長さ
このとき,
(東京大)

東京大学(2004)の問題です.東大では他にも放物線上に3点をとって三角形を考えさせる問題(例えば1982年 ) があります.もともとは旧課程にあった行列を利用して解く問題でしたが,現行過程では複素平面で扱う極形式を用いて同じことができます.要するに,ある点を別の点を中心として回転移動させるという操作が必要になってくるのです.
解答
■
直線PQの傾きが
展開して
整理して
よって
ただし
とおいた.
ここで,3点P,Q,Rを複素平面上に移して,順に3点
と考えることができる.原点を中心とする
と表せる.この式の右辺を左から順に計算していくと,
上で
と表せる.よって
故に点
となる.Rも放物線
右辺を展開して
整理して
両辺を
①を代入して
整理して
よって
故に
補足
一般に,傾き
と表されます.
証明
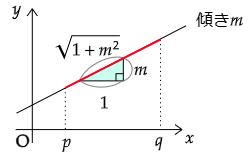
底辺が1,高さが
■
Rが弧PQ上にあるとすれば,
となることに加えて,直線PQの傾きが
|PQの傾き|>|PRの傾き|
となって,PQ=PRとなることができません.
