高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | |||
| 2. 複素数が表す図形 | |||
| 3. 極形式 | |||
| 4. ド・モアブルの定理 | |||
| 5. 複素数と図形 |

3. 極形式
3.1 極形式とは
複素数の新しい表現法~具体例
例えば,複素数 $z=1+\sqrt 3i$ は複素平面上で次の点を表す.
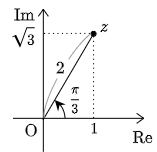
この実部の $1$ と虚部の $\sqrt3$ は,三角関数のところで学んだように原点からの距離2と実軸からの回転角 $\dfrac\pi3$ によって
\[1=2\cos\dfrac\pi3,\ \ \sqrt3=2\sin\dfrac\pi3\]
というようにも表すことができるから
\[z=2\cos\dfrac\pi3+\left(2\sin\dfrac\pi3\right)i\]
とも表現できる.2でくくって
\[z=2\left(\cos\dfrac\pi3+i\sin\dfrac\pi3\right)\]
これが複素数 $z$ の新しい表現法である.つまりこの複素数 $z$ は
\[1+\sqrt3=2\left(\cos\dfrac\pi3+i\sin\dfrac\pi3\right)\]
という2通りの表し方ができるようになったのだ.

複素数の新しい表現法~一般論
$a,\ b$ を実数として,複素平面上の原点O以外の点 $z=a+b\,i$ は次のような点を表すのであった.
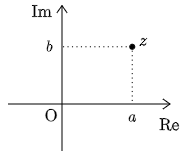
今この実部と虚部である $a,\ b$ を異なる方法で表すことを考える.そうすることで,複素数の取り扱いが驚くほど簡単になる上に,複素平面において,回転移動という変換がとても考えやすくなるのである.

複素平面上の原点O以外の点 $z$ を,Oからの距離 $r$ と,実軸の正の向きからの回転角 $\theta$ で表すことを考える.ただし,反時計回りを正の向き,時計回りを負の向きとし,角度は弧度法 を用いる.
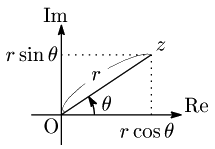
図から複素数 $z$ の実部は $r\cos\theta$,虚部は $r\sin\theta$ と表されることがわかる.この辺りの考え方は三角関数のところで十分習熟していることであろう.従って $z$ は
\[z=r\cos\theta+i\,r\sin\theta\]
と表せる.$r$ でくくって
\[z=r(\cos\theta+i\sin\theta)\]
複素数のこのような表し方を極形式(きょくけいしき)という.
極形式
\[ z=r(\cos\theta +i\sin\theta)\]
$i$ が $+$ のすぐあとにきているのが気になるかもしれないが,これは $z=r(\cos\theta+\sin\theta\,i)$ と書いたのでは,$\sin(\theta\,i)$ と紛らわしいため,通常このような記法をとる.どうしても $i$ を最後に書きたい場合は,$(\sin\theta)\,i$ のように $i$ が $\sin\theta$ の中に入っていないことがはっきりとわかるように書かなくてはならない.
このときの角 $\theta$ を偏角(へんかく)といい,$\boldsymbol{{\rm arg}\,z}$ で表す.
\[{\rm arg}\ z=\theta\]
この arg というのは英語で偏角を意味する argument からきている.
また,複素数 $z$ の絶対値 $|z|$ は,複素平面上において原点からの距離を表していたから
\[|z|=r\]
である.これは計算によっても
\[|z|=|r|\sqrt{\cos^2\theta+\sin^2\theta}=|r|=r\]
となることから確かめられる.
まとめ\[ r=|z|,\ \ \theta ={\rm arg}\, z \]
補足
例えば,${\rm arg}\,(1-i)$ は $\dfrac 74\pi$ でも $-\dfrac\pi4$ でもよい.つまり,$2\pi$ の整数倍の差がある2つを同一視する.
${\rm arg}\,z_1={\rm arg}\,z_2$ というときは,$2\pi$ の整数倍の違いを無視して一致することを意味する.
例
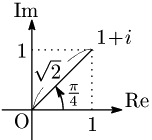
$z=1+i$ のとき,$|z|=\sqrt2$,${\rm arg}\,z=\dfrac\pi4$ により,
\[z=\sqrt2\left(\cos\frac\pi4+i\sin\frac\pi4\right)\]
例題 複素数 $z$ が極形式で $z=r(\cos\theta+i\sin\theta)$ と表されているとき, $z$ の共役 $\overline{z}$ を極形式で表せ.
こたえ
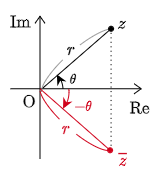
図より,
$|\overline{z}|=r,\ \ \ \ {\rm arg}\,\overline{z}=-\theta$
であるから
\[\overline{z}=r\{\cos(-\theta)+i\sin(-\theta)\}\]
$z$ が実数や純虚数となる条件
複素数 $z$ が実数や純虚数となる条件を,偏角という観点から見ていこう.ただし,偏角 $\theta$ は $0\leqq\theta<2\pi$ とする.
複素平面上において,
$z$ が実数 $\iff z$ は実軸上
であったから,実軸上にある複素数の偏角は,原点を除き $0$ か $\pi$ である.
また,$z$ が0でなければ
$z$ が純虚数 $\iff z$ は虚軸上
であったから,虚軸上にある複素数の偏角は,原点を除き $\dfrac\pi2$ か $\dfrac32\pi$ である.
定理 0でない複素数 $z$ について,偏角が0以上 $2\pi$ 未満のとき
$z$ が実数 $\iff$ ${\rm arg}\ z=0$ or $\pi$
$z$ が純虚数 $\iff$ ${\rm arg}\ z=\dfrac\pi 2$ or $\dfrac 32\pi$

3.2 複素数の乗法・除法
次の例題を考えてみよう.
例題 2つの複素数 $z_1=1+\sqrt3\,i$,$z_2=1+i$ について,$z_1z_2$,$\dfrac{z_1}{z_2}$ をそれぞれ極形式で表せ.
$z_1z_2$ から考えていこう.これを極形式で表すには $z_1z_2$ という複素数について,原点からの距離,すなわち $|z_1z_2|$ と,偏角 ${\rm arg}\ z_1z_2$ の情報が必要である.$z_1z_2$ を実際に計算してみると
\[\begin{align*}
z_1z_2&=(1+\sqrt3\,i)(1+i)\\[5pt]
&=(1-\sqrt3)+(1+\sqrt3)i
\end{align*}\]
となるから
\[|z_1z_2|=\sqrt{(1-\sqrt3)^2+(1+\sqrt3)^2}=\sqrt8=2\sqrt2\]
である.一方,偏角 ${\rm arg}\ z_1z_2$ の方はというと,下の図のように複素平面上に点 $z_1z_2$ を何となくとってみても,偏角はよくわからない.
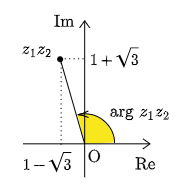
これ以上はお手上げになってしまった.
極形式なら打開できる
上の例題では $z_1z_2$ の絶対値は計算できても,偏角の方がよくわからず,結局 $z_1z_2$ を極形式で表すことは叶わなかった.ところが実は $z_1$ と $z_2$ を最初の段階で極形式で表しておけば,事態が打開できるのである.