高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | |||
| 2. 複素数が表す図形 | |||
| 3. 極形式 | |||
| 4. ド・モアブルの定理 | |||
| 5. 複素数と図形 |

4. ド・モアブルの定理
4.1 ド・モアブルの定理とは
極形式の節で学んだように,極形式で表された2つの複素数
\[z_1=r_1(\cos\theta_1+i\sin\theta_1),\ z_2=r_2(\cos\theta_2+i\sin\theta_2)\]
について,
\[z_1z_2=r_1r_2\{\sin(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\}\]
となるから,$z=\cos\theta+i\sin\theta$ のとき,
\[\begin{align*} z^2&=\cos(\theta+\theta)+i\sin(\theta+\theta)\\[5pt] &=\cos2\theta+i\sin2\theta\\[5pt] z^3&=z^2\cdot z\\[5pt] &=\cos(2\theta+\theta)+i\sin(2\theta+\theta)\\[5pt] &=\cos3\theta+i\sin3\theta \end{align*}\]
また,
\[\begin{align*}
\frac1z&=\frac{\cos0+i\sin0}{\cos\theta+i\sin\theta}\\[5pt]
&=\cos(0-\theta)+i\sin(0-\theta)\\[5pt]
&=\cos(-\theta)+i\sin(-\theta)\\[5pt]
\frac1{z^2}&=\frac{\cos0+i\sin0}{\cos2\theta+i\sin2\theta}\\[5pt]
&=\cos(0-2\theta)+i\sin(0-2\theta)\\[5pt]
&=\cos(-2\theta)+i\sin(-2\theta)\\[5pt]
\frac1{z^3}&=\frac{\cos0+i\sin0}{\cos3\theta+i\sin3\theta}\\[5pt]
&=\cos(0-3\theta)+i\sin(0-3\theta)\\[5pt]
&=\cos(-3\theta)+i\sin(-3\theta)\\[5pt]
\end{align*}\]
従って,複素数 $z$,及び自然数 $n$ に対して,$z^{-n}$ を $\dfrac1{z^n}$,$z^0=1$ と定義すれば,一般に次が成り立つ:
ド・モアブルの定理 $n$ が整数のとき,
\[ (\cos\theta +i\sin\theta)^n=\cos n\theta +i\sin n\theta \]

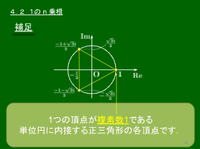
4.2 1の $n$ 乗根
※ 「$n$ 乗根(累乗根)」についての復習はこちら.