座標平面の基礎｜内分・外分・2点間の距離・対称点・三角形の重心をスライドでやさしく解説【高校数学】

高校数学[総目次]

数学Ⅱ　第3章　図形と方程式

	スライド	ノート	問題
1. 座標平面上の点
2. 直線の方程式
3. 円の方程式
4. 円と直線
5. 軌跡と方程式
6. 不等式と領域

1．座標平面上の点

1.1　数直線上の点

　数直線上の1点をPとするとき，Pに対応する実数 $x$ をPの座標といい，${\rm P}(x)$ で表す．例えば下の図では点Pが2に対応しているから ${\rm P}(2)$ と表す．

　数直線上に2点A，Bをとり，線分ABを考える．この線分を $m:n$ に分ける方法として，内分と外分を説明する．内分の方は特に問題ないだろうが，外分の方は少しわかりにくいので注意を要する．

　内分や外分の概念は，数直線上の線分に限らず，一般の線分に対して定義されるが，ここでは数直線上の線分に限定して話を進める．

内分点

　数直線上の2点A，Bについて，線分AB上に点Pがあるとする．このとき，${\rm AP:PB=}m:n$ であるならば，点Pは線分ABを $m:n$ に内分するといい，Pを内分点（ないぶんてん）という．

注意

　例えば $1:2$ に内分するといっても「線分ABを $1:2$ に内分する」というのと「線分BAを $1:2$ に内分する」というのは異なる．要するにAとBのどちらの点を先に述べるかということである．

　数直線上の2点 ${\rm A}(a)$，${\rm B}(b)$ について，線分ABを $m:n$ に内分する点 ${\rm P}$ の座標 $x$ を求めてみよう．

1°　$a<b$ のとき

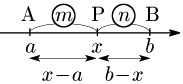
$$\begin{align*} (x-a):(b-x)&=m:n\\[5pt] n(x-a)&=m(b-x)\\[5pt] (m+n)x&=na+mb\\[5pt] \therefore x&=\frac{na+mb}{m+n} \end{align*}$$

2°　$a>b$ のとき

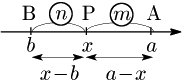
$$\begin{align*} (a-x):(x-b)&=m:n\\[5pt] n(a-x)&=m(x-b)\\[5pt] (m+n)x&=na+mb\\[5pt] \therefore x&=\frac{na+mb}{m+n} \end{align*}$$

　1°，2° ともに同じ結果となるから次が成り立つ：

内分点　数直線上の2点A$(a)$, B$(b)$について，線分ABを$m:n$に内分する点の座標は， $$\frac{na+mb}{m+n}$$ 　特に，線分ABの中点（$1:1$に内分する点）の座標は， $$\frac{a+b}2$$

例　　数直線上の2点 ${\rm A}(3)$，${\rm B}(6)$ について，

(1) 線分ABを $2:1$ に内分する点の座標

$$\frac{1\times3+2\times6}{2+1}=5$$

(2) 線分ABの中点

$$\frac{3+6}2=\frac92$$

外分点

　数直線上の2点A，Bについて，数直線上の線分ABの外側に点Qがあるとする．このとき，${\rm AQ:QB=}m:n$ であるならば，点Qは線分ABを $m:n$ に外分するといい，Pを外分点（がいぶんてん）という．

　内分のときと違って外分は少し難しい．数直線上の2点A，Bをとって線分ABを考えるところまでは同じなのであるが，内分のときには点Pを線分AB上にとったのに対し，外分では数直線上の線分AB以外のところ，つまり外側にとるのである．

　外分を理解するために，「線分ABを $2:1$ に外分する点P」と「線分ABを $1:2$ に外分する点Q」の2つを例にとろう．ポイントは「ひと筆書き」である．

1°　線分ABを $2:1$ に外分する点P

　数直線上のAに鉛筆を置き，そこから数直線に沿って2だけ進んだところにPを書く．ただしPは線分ABの外側にとる．そして鉛筆を浮かすことなくそこから1だけ移動させるとBにたどり着く．そのような点Pが線分ABを $2:1$ に外分する点である．

2°　線分ABを $1:2$ に外分する点Q

　数直線上のAに鉛筆を置き，そこから数直線に沿って1だけ進んだところにQを書く．ただしQは線分ABの外側にとる．そして鉛筆を浮かすことなくそこから2だけ移動させるとBにたどり着く．そのような点Qが線分ABを $1:2$ に外分する点である．

　アニメーションの鉛筆の動きからわかるように，$m:n$ に外分するというときの外分点の位置は，$m>n$ ならばAからBに向かう側にあり，逆に $m<n$ ならばBから遠ざかる側にある．

　数直線上の2点 ${\rm A}(a)$，${\rm B}(b)$ について，線分ABを $m:n$ に外分する点 ${\rm Q}$ の座標 $x$ を求めてみよう．

1°　$m>n$ のとき

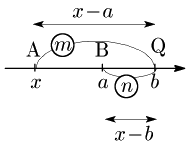
$$\begin{align*} (x-a):(x-b)&=m:n\\[5pt] m(x-b)&=n(x-a)\\[5pt] (m-n)x&=-na+mb\\[5pt] \therefore x&=\frac{-na+mb}{m-n} \end{align*}$$

2°　$m<n$ のとき

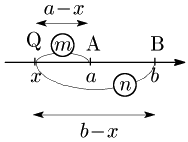
$$\begin{align*} (a-x):(b-x)&=m:n\\[5pt] n(a-x)&=m(b-x)\\[5pt] (m-n)x&=-na+mb\\[5pt] \therefore x&=\frac{-na+mb}{m-n} \end{align*}$$

　1°，2° ともに同じ結果となるから次が成り立つ：

外分点　数直線上の2点A$(a)$, B$(b)$について，線分ABを$m:n$に外分する点の座標は，($m$と$n$の大小関係によらず) $$\frac{-na+mb}{m-n}$$

例　　数直線上の2点 ${\rm A}(3)$，${\rm B}(5)$ について，

(1) 線分ABを $2:1$ に外分する点の座標

$$\frac{-1\times3+2\times5}{2-1}=7$$

(2) 線分ABを $1:2$ に外分する点の座標

$$\frac{-2\times3+1\times5}{1-2}=1$$

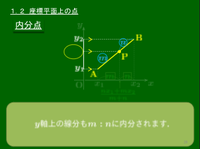
1.2　座標平面上の点

2点間の距離

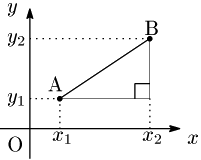
　2点 ${\rm A}(x_1,y_1)$，${\rm B}(x_2,y_2)$ について，2点A，B間の距離ABは，三平方の定理により，

$${\rm AB}^2=(x_2-x_1)^2+(y_2-y_1)^2$$

となる．この式は，ABが $x$ 軸に垂直な場合($x_1=x_2$)や，$y$ 軸に垂直な場合($y_1=y_2$)でも成り立つ．
　${\rm AB}>0$ であるから，

$${\rm AB}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$

　特に，点Bが原点 ${\rm O}(0,0)$ のとき，

$${\rm OA}=\sqrt{{x_1}^2+{y_1}^2}$$

2点間の距離　平面上の2点A$(x_1,y_1)$, B$(x_2,y_2)$について，2点間の距離ABは， $${\rm AB}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$ 　特に，Bが原点$(0,0)$のとき， $${\rm OA}=\sqrt{{x_1}^2+{y_1}^2}$$

例　　A$(1,4)$，B$(3,2)$ のとき，

$$\begin{align*} {\rm AB}&=\sqrt{(3-1)^2+(2-4)^2}\\[5pt] &=\sqrt8\\[5pt] &=\underline{\boldsymbol{2\sqrt2}} \end{align*}$$

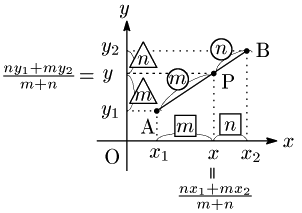
内分点・外分点

　平面上の2点 ${\rm A}(x_1,y_1)$，${\rm B}(x_2,y_2)$ について

1° 線分ABを $m:n$ に内分する点P

2° 線分ABを $m:n$ に外分する点Q

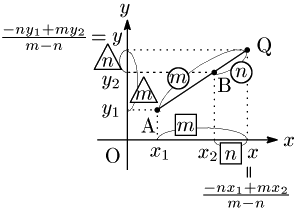
　平行線と線分の比の関係を考えると，結局数直線上の2点の場合に帰着される．

まとめ　平面上の2点A$(x_1,y_1)$, B$(x_2,y_2)$ について，線分ABを $m:n$ に $$\begin{align*}&\mbox{内分する点}:\left(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\right)\\ &\hspace{10mm}\mbox{特に中点は}\left(\frac{x_1+x_2}2,\frac{y_1+y_2}2\right)\\ &\mbox{外分する点}:\left(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n}\right)\end{align*}$$

例　平面上の2点 ${\rm A}(0,1)$，${\rm B}(3,4)$ について

(1) $2:1$ に内分する点

$$\left(\frac{1\cdot0+2\cdot3}{2+1},\frac{1\cdot1+2\cdot4}{2+1}\right)$$

$$\therefore (2,3)$$

(2) 中点

$$\left(\frac{0+3}2,\frac{1+4}2\right)$$

$$\therefore \left(\frac32,\frac52\right)$$

(3) $4:1$ に外分する点

$$\left(\frac{-1\cdot0+4\cdot3}{4-1},\frac{-1\cdot1+4\cdot4}{4-1}\right)$$

$$\therefore (4,5)$$

(4) $1:4$ に外分する点

$$\left(\frac{-4\cdot0+1\cdot3}{1-4},\frac{-4\cdot1+1\cdot4}{1-4}\right)$$

$$\therefore (-1,0)$$

対称な点

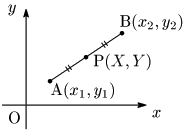
　2点A$(x_1,y_1)$，B$(x_2,y_2)$ が点P$(X,Y)$ に関して対称な位置にあるとき，

点Pは線分ABの中点

と捉える．

例題　点A$(1,4)$と，点P$(3,2)$に関して対称な点Bの座標は？

　点P$(3,2)$ は線分ABの中点だから，

$$\left\{ \begin{array}{ll} \dfrac{1+x}2=3\\[5pt] \dfrac{4+y}2=2 \end{array}\right. \ \ \ \therefore \left\{ \begin{array}{ll} x=5\\[5pt] y=0 \end{array}\right.$$

　よって，B$\boldsymbol{(5,0)}$

三角形の重心

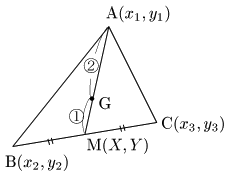
　辺BCの中点をM$(X,Y)$ とおくと，

$$\left\{ \begin{array}{ll} X=\dfrac{x_2+x_3}2\\[5pt] Y=\dfrac{y_2+y_3}2 \end{array}\right.$$

　重心Gは，線分AMを $2:1$ に内分する点であるから，G$(x,y)$ は，

$$\left\{ \begin{array}{ll} x=\dfrac{1\cdot x_1+2X}{2+1}=\dfrac{x_1+x_2+x_3}3\\[5pt] y=\dfrac{1\cdot y_1+2Y}{2+1}=\dfrac{y_1+y_2+y_3}3 \end{array}\right.$$

まとめ　3点A$(x_1,y_1)$, B$(x_2,y_2)$, C$(x_3,y_3)$について，△ABCの重心の座標は， $$\left(\frac{x_1+x_2+x_3}3,\ \frac{y_1+y_2+y_3}3\right)$$

---

高校数学[総目次]

数学Ⅱ　第3章　図形と方程式

	スライド	ノート	問題
1. 座標平面上の点
2. 直線の方程式
3. 円の方程式
4. 円と直線
5. 軌跡と方程式
6. 不等式と領域