高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | |
| 1. 座標平面上の点 | [無料] | |
| 2. 直線の方程式 | [無料] | |
| 3. 円の方程式 | [会員] | |
| 4. 円と直線 | [会員] | |
| 5. 軌跡と方程式 | [会員] | |
| 6. 不等式と領域 | [会員] |
6.1 不等式の表す領域
例 $y>x+1$ の表す領域を考える．
$x=-1$ のとき，$y>0$
$x=0$ のとき，$y>1$
$x=1$ のとき，$y>2$
$x=2$ のとき，$y>3$
$\vdots$
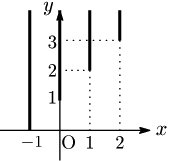
$x$ がすべての実数をとると，$y>x+1$ の表す領域は図の斜線領域である．ただし，境界線は含まない．
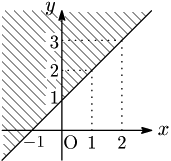
補足
図の境界線には，可能な範囲でそのグラフから方程式が復元できるように通過点などを書き込んでおく．例えば，
直線 ：2点
円 ：中心と半径がわかるようにしておく
放物線：頂点ともう1点
など．
一般に不等式の表す領域は次のようになる：
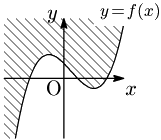
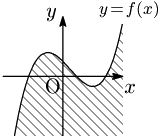
注意
不等式の表す領域は，通常斜線で図示する．その際，境界線を含む，含まないについてのコメントも必ず添えておく．
発展的補足
例えば，$y\boldsymbol{>}x+1$ の表す領域に属する任意の点を $(x_1,y_1)$ とすると，$y_1>x_1+1$，即ち \[x_1-y_1+1<0\] が成り立つ．
また，$y\boldsymbol{<}x+1$ の表す領域に属する任意の点を $(x_2,y_2)$ とすると，$y_2<x_2+1$，即ち \[x_2-y_2+1>0\] が成り立つ．
つまり，直線 $x-y+1=0$ に関して異なる領域に属する2点の座標を $x-y+1$ に代入すると，式の値は異符号になる．この事実は例えば「直線が座標平面上の2点の間を通過する」といった条件で利用される．
$x>h,\ y>k\ (h,k$ は定数)の表す領域
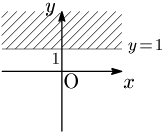
例1 $x<-1$
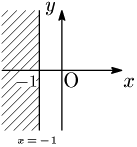
例1 $y\geqq1$
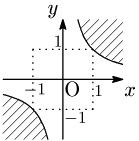
例題 不等式 $xy>1$の表す領域を図示せよ．
こたえ
解答例を表示する
補足
$y>\dfrac1x$ の表す領域とは異なる：
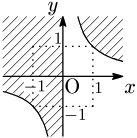
(境界線を含まない)
6.2 円の内部・外部
例題 不等式 $(x\!-\!1)^2\!+\!(y\!-\!2)^2\!\leqq\!3^2$ の表す領域を図示せよ．
P$(x,y)$ ，C$(1,2)$ とすると，与式は \[\begin{align*} {\rm CP}^2&\leqq3^2\\[5pt] \therefore {\rm CP}&\leqq3 \end{align*}\] よって与式を満たすPは，円 $(x\!-\!1)^2\!+\!(y\!-\!2)^2\!=\!3^2$ の周及び内部にある．
従って，与式の表す領域は図の境界線を含む斜線部分である：
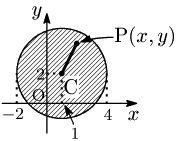
一般に次が成り立つ：
[1] $(x-a)^2+(y-b)^2<r^2$
→ 円①の内部
[2] $(x-a)^2+(y-b)^2>r^2$
→ 円①の外部
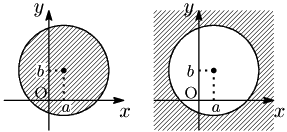
ともに境界線を含まない．
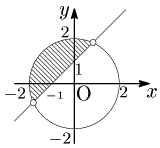
例題 連立不等式$\left\{\begin{array}{l}y> x+1\\x^2+y^2\leqq 4\end{array}\right.$ の表す領域を図示せよ．
答
解答例を表示する
6.3 線形計画法
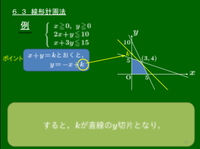
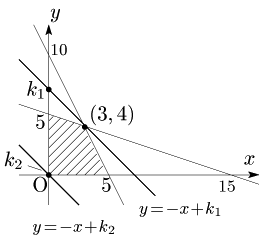
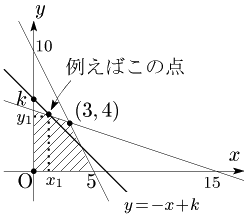
例題 $x,y$ が次の不等式 \[\left\{\begin{array}{l}x\geqq0,\ y\geqq0\\ 2x+y\leqq10\\ x+3y\leqq15 \end{array}\right.\] を満たすとき，$x+y$ の最大値と最小値を求めよ．
前提となる考え方
例えば，$x+y=5$ となる $(x,y)$ の組は無数にあるが，それらの組1つ1つを座標平面上に落としていくと，1つの図形が浮かび上がる．それは即ち直線 $y=-x+5$ である．この直線上の任意の点 $(x,y)$ について，$x+y$ の値は5になり，その値は $y$ 切片に現れる．和が5になる $(x,y)$ の組は漏れなくこの直線上にあるのであり，この直線上以外の点 $(x,y)$ は決して $x+y$ が5にならない．
ポイント
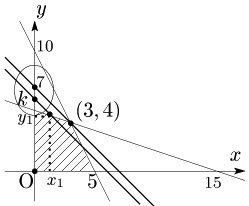
$x+y=k$ とおく．
→ 直線を表し，$k$ はその $y$ 切片
境界線の傾きに注意して $k$ を動かす
答
解答例を表示する
よくある質問
-
何故，点 $(3,4)$ を通るときが最大か．例えば図のような点を通るときが最大でない理由は？
-
指定した点 $(x_1,y_1)$ について，$x_1+y_1$ の値が $k$ だとすれば，この $k$ は上の図で直線 $y=-x+k$ の $y$ 切片となって現れている．しかしこの $k$ は，下図の $y$ 軸上を見れば，7より小さい．従って，$x_1+y_1(=k)$ は最大ではない．
6.4 命題と領域
「$p$ ならば $q$」を「$p\Rightarrow q$」と書く．
「$p\Rightarrow q$」が真であることを示すためには，「$\boldsymbol p$ を満たすどれをとっても $\boldsymbol q$ を満たす」ことを示さなければならない．ここに集合の考え方が役立つ．
条件 $p,q$ の真理集合をそれぞれ $P,Q$ とすると，
$p\Rightarrow q$ が真 $\iff P\subset Q$
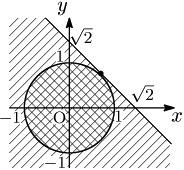
例題 $x^2+y^2\leqq1$ ならば $x+y\leqq\sqrt2$ を示せ．
答
解答例を表示する
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | |
| 1. 座標平面上の点 | [無料] | |
| 2. 直線の方程式 | [無料] | |
| 3. 円の方程式 | [会員] | |
| 4. 円と直線 | [会員] | |
| 5. 軌跡と方程式 | [会員] | |
| 6. 不等式と領域 | [会員] |