5. 軌跡と方程式(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第3章　図形と方程式

	スライド	ノート
1. 座標平面上の点	[無料]
2. 直線の方程式	[無料]
3. 円の方程式	[会員]
4. 円と直線	[会員]
5. 軌跡と方程式	[会員]
6. 不等式と領域	[会員]

5.1　軌跡

軌跡とは？

　ある条件を満たす点全体が全体が作る図形

例1　条件：定点Cから一定の距離 $r$ にある
　　　→　軌跡は中心C，半径 $r$ の円

例2　条件：2点A，Bから等距離にある
　　　→　軌跡は線分ABの垂直二等分線

5.2　軌跡の求め方

　ある条件Cを満たす点Pの軌跡が図形Fであるとは，

条件Cを満たす点Pの軌跡$\iff$図形F

を意味する．従って，　　　を示すには，

[1] 「$\Rightarrow$」即ち条件Cを満たす点はすべて図形F上にある．(必要条件)

[2] 「$\Leftarrow$」即ち図形F上の点はすべて条件Cを満たす．(十分条件)

の2つを示さなければならない．

例題　2点A$(0,1)$とB$(3,4)$から等距離にある点P$(x,y)$の軌跡を求めよ．

[1](必要性)
　AP$=$BP $\cdots$ ①より，AP$^2=$BP$^2\ \cdots$②
　従って，$x^2\!+\!(y\!-\!1)^2\!=\!(x\!-\!3)^2\!+\!(y\!-\!4)^2\ \cdots$③
　整理して，$x+y-4=0\ \cdots$④
　よって条件を満たす点は，直線④上にある．

[2](十分性)
　直線④上の点は③を満たし，
　③は②を意味し，
　AP$>0$，BP$>0$ であるから ②$\Rightarrow$①

　[1]，[2]より，点P$(x,y)$ について，

AP$=$BP $\iff x+y-4=0$

よって求める軌跡は，直線 $\boldsymbol{x+y-4=0}$

補足

　[2]については本問のように計算の逆をたどることで成り立つことが明らかならば省略することも多い．

[2]に注意を要する例

例題　線分ABを底辺とする二等辺三角形の頂点Pの軌跡を求めよ．

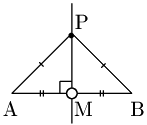
[1]　AP$=$BPよりPは線分ABの垂直二等分線上にあることが必要．

[2]　線分ABの垂直二等分線上の点のうち，線分ABの中点Mを除けば△PABは二等辺三角形．

[1]，[2]により，求める軌跡は線分ABの垂直二等分線(ただし線分ABの中点を除く．)

5.3　いくつかの例題

例題1　2点A$(0,0)$，B$(3,0)$ からの距離の比が $2:1$ である点Pの軌跡を求めよ．

答

　解答例を表示する >

　P$(X,Y)$ とする．条件より
　　　　AP:BP$=2:1$
　　　　∴　AP$=2$BP
　両辺を2乗して，
　　　　　AP$^2=$4BP$^2$
　∴　$X^2+Y^2=4\{(X-3)^2+Y^2\}$
　展開して整理すると，
　　　$X^2+Y^2-8X+12=0$
　　∴　$(X-4)^2+Y^2=2^2$
　これは点P$(X,Y)$ が，円 $(x-4)^2+y^2=2^2\ \cdots$① 上にあることを意味する．
　逆に，円①上の任意の点は条件を満たす．
　よって求める軌跡は，点 $\boldsymbol{(4,0)}$ を中心とする半径2の円．

補足

　一般に，$m\neq n$ のとき，2点A，Bからの距離の比が $m:n$ である点Pの軌跡は，線分ABを $m:n$ に内分，及び外分する2点を直径の両端とする円になる．この円をアポロニウスの円という．

例題2　$a$ が実数全体をとるとき，放物線 $y=x^2-2ax+1$ の頂点Pの軌跡を求めよ．

答

　解答例を表示する >

\[\begin{align*} y&=x^2-2ax+1\\[5pt] &=(x-a)^2-a^2+1 \end{align*}\] 　よって頂点Pの座標は，$(a,-a^2+1)$．
　P$(X,Y)$ とすると， \[\left\{\begin{array}{ll} X=a&\cdots\mbox{①}\\[5pt] Y=-a^2+1&\cdots\mbox{②} \end{array}\right.\] 　①より，$a=X$．これを②に代入して， \[Y=-X^2+1\] 　よって点P$(X,Y)$ は放物線 $y=-x^2+1\ \cdots$③ 上にある．
　逆に，放物線③上の任意の点は条件を満たす．
　よって求める軌跡は，放物線 $\boldsymbol{y=-x^2+1}$

例題3　円 $x^2+y^2=4$ 上の動点 Q と，点A$(4,0)$ について，線分AQの中点Pの軌跡を求めよ．

答

　解答例を表示する >

　P$(X,Y)$，Q$(s,t)$ とする．
　Qは円 $x^2+y^2=4$ 上の点であるから，
　　　　$s^2+t^2=4\ \cdots$①
　Pの座標は， \[\left\{\begin{array}{l} X=\dfrac{4+s}2\\[5pt] Y=\dfrac{0+t}2 \end{array}\right. \ \ \ \therefore \left\{\begin{array}{l} s=2X-4\\[5pt] t=2Y \end{array}\right.\] 　これらを①に代入して， \[\begin{align*} (2X-4)^2+(2Y)^2&=4\\[5pt] \therefore (X-2)^2+Y^2&=1 \end{align*}\] 　よって，点P$(X,Y)$ は，円 $(x-2)^2+y^2=1\ \cdots$① 上にある．
　逆に，円①上の任意の点は条件を満たす．
　よって求める軌跡は，点$\boldsymbol{(2,0)}$ を中心とする半径1の円．

---

高校数学[総目次]

数学Ⅱ　第3章　図形と方程式

	スライド	ノート
1. 座標平面上の点	[無料]
2. 直線の方程式	[無料]
3. 円の方程式	[会員]
4. 円と直線	[会員]
5. 軌跡と方程式	[会員]
6. 不等式と領域	[会員]