高校数学[総目次]
数学A 第2章 確率
| スライド | ノート | 問題 | |
| 1. 事象と確率 | |||
| 2. 確率の基本性質 | |||
| 3. 独立な試行の確率 | |||
| 4. 反復試行の確率 | |||
| 5. 条件付き確率 |

2. 確率の基本性質
2.1 積事象と和事象
全事象を表す集合を $U$,事象 $A$,$B$ を表す $U$ の部分集合をそれぞれ $A$,$B$ とする.
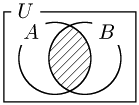
積事象
「事象 $A$,$B$ がともに起こる」という事象で,
\[A\cap B\]
で表す.
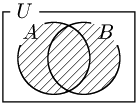
和事象
「事象 $A$ または $B$ が起こる」という事象で,
\[A\cup B\]
で表す.

2.2 排反事象
例 さいころを1回だけ投げる場合
事象A:奇数の目が出る → $A=\{1,3,5\}$
事象B:2の目が出る → $B=\{2\}$
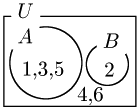
この2つの事象は同時には起こらない.このとき,事象AとBは互いに排反であるという.
即ち排反とは,$A\cap B=\varnothing$ となるときをいう.

2.3 確率の基本性質
全部の場合 :$n$ 通り(同様に確からしい)
事象Aの起こる場合:$a$ 通り
$0\leqq a\leqq n$ であるから,
\[\frac0n\leqq \frac an\leqq \frac nn\] \[\therefore 0\leqq P(A)\leqq 1\]
補足
左辺の $\dfrac 0n$ 即ち $0$ は空事象の確率,右辺の $\dfrac nn$ 即ち $1$ は全事象の確率を表す.
確率の基本性質 $U$ を全事象,$A$ をある事象とするとき,\begin{align*} &[1]\ \ 0\leqq P(A) \leqq 1\\[5pt] &[2]\ \ P(\varnothing)\!=\!0,\ \ P(U)\!=\!1\\ \end{align*}

2.4 和事象の確率
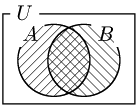
\[n(A\cup B)=n(A)+n(B)-n(A\cap B)\]
この両辺を $n(U)$ で割ると,
\[\frac{n(A\cup B)}{n(U)}=\frac{n(A)}{n(U)}+\frac{n(B)}{n(U)}-\frac{n(A\cap B)}{n(U)}\]
\[\therefore P(A\cup B)=P(A)+P(B)+P(A\cap B)\]
特に,事象 $A$ と事象 $B$ が同時に起こらない,すなわち排反のとき,$A\cap B=\varnothing$ であるから,$P(A\cap B)=0$.よって,
\[P(A\cup B)=P(A)+P(B)\]
和事象の確率 2つの事象 $A,\ B$ について,\[P(A\cup B)=P(A)+P(B)-P(A\cap B)\] 特に $A$ と $B$ が排反のとき,\[P(A\cup B)=P(A)+P(B)\]
例題 さいころを1回投げるとき,偶数の目が出る,または4以上の目が出る確率を求めよ.
答
全事象U:$U=\{1,2,3,4,5,6\}$
事象A「偶数の目が出る」:$A=\{2,4,6\}$
事象B「4以上の目が出る」:$B=\{4,5,6\}$
事象AかつB「偶数かつ4以上」:$A\cap B=\{4,6\}$
確率はそれぞれ
\[\begin{align*}
P(A)&=\frac36=\frac12\\[5pt]
P(B)&=\frac36=\frac12\\[5pt]
P(A\cap B)&=\frac26=13
\end{align*}\]
よって,
\[\begin{align*}
P(A\cup B)&=P(A)+P(B)-P(A\cap B)\\[5pt]
&=\frac12+\frac12-\frac13\\[5pt]
&=\underline{\boldsymbol {\frac23}}
\end{align*}\]
補足
直接計算すれば,$A\cup B=\{2,4,5,6\}$ より,
\[P(A\cup B)=\frac46=\underline{\boldsymbol{\frac23}}\]


