5. 条件付き確率(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学A　第2章　確率

	スライド	ノート
1. 事象と確率	[無料]
2. 確率の基本性質	[無料]
3. 独立な試行の確率	[会員]
4. 反復試行の確率	[会員]
5. 条件付き確率	[会員]

5. 条件付き確率

5.1　条件付き確率

　事象$A$ が起こるという条件の下で，事象$B$ が起こる確率を，条件付き確率といい， \[P_A(B)\] で表す．条件付き確率はその意味から簡単に求まるタイプとそうでないタイプの2つがある．条件付き確率が簡単に求まる例として次のようなものがある．

例題1　10本中の3本が当たりのくじを1本ずつ引く．1本目が当たりであるという条件のもと，2本目も当たりである条件付き確率を求めよ．

こたえ

　1本目が当たりであるという条件を付けたので，2本目を引くときには当たりくじが1本減って2本となっている．従って求める条件付き確率は，9本中の2本が当たりであるくじを引いて当たりが出る確率だから，

$\dfrac29\ \ \cdots$ (答)

　一方，次の例題はどうだろう．

例題2　10本中の3本が当たりのくじを1本ずつ引く．2本目が当たりであるという条件のもと，1本目も当たりであった条件付き確率を求めよ．

　例題1と違ってこちらの条件付き確率はさっぱりわからない．（1本目と2本目の両方が当たりの場合と，1本目がハズレで2本目が当たりの場合の2通りがあるから求める条件付き確率は $\dfrac12$ というのは間違い．）

　条件付き確率 $P_A(B)$ が簡単にわからない場合は，次の定義式から計算することになる：

　例題2の解答は，「2本目に当たりが出る」という事象を $A$，「1本目に当たりが出る」という事象を $B$ とすると，

\[\begin{align*} &P(A)=\frac3{10}\\[5pt] &P(A\cap B)=\frac{_3{\rm P}_2}{_{10}{\rm P}_2}=\frac1{15} \end{align*}\]

　よって求める条件付き確率は，

$\dfrac{\dfrac1{15}}{\dfrac3{10}}=\dfrac29\ \ \cdots$ (答)

補足

　例題1を条件付き確率の定義式から求めると，

\[\frac{\dfrac{_3{\rm P}_2}{_{10}{\rm P}_2}}{\dfrac3{10}}=\frac{\dfrac{3\cdot2}{10\cdot9}}{\dfrac3{10}}=\frac29\]

　例題1と2の結果が同じ値となったが，だからと言って $P_A(B)=P_B(A)$ が常に成り立つわけではない．

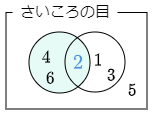
　条件付き確率 $P_A(B)$ の定義式を見ればわかるように，「分母の確率に占める分子の確率の割合」というのが条件付き確率の本質であって，とりわけ同様に確からしい場合には「事象$A$ が起こる場合のうち，事象$B$ も起こる割合」として計算できることわかる．例えば「さいころを1回投げて偶数の目が出るという条件のもと，3以下の目が出るという条件付き確率」を考えてみよう．偶数の目の出方は2，4，6の3通りでこれらは同様に確からしい．このうち3以下の目は2の1通りであるから，求める条件付き確率は

\[\frac13\]

となる．

例題　大小2つのさいころを投げたとき，ともに3以下の目が出たという条件のもと，出た目の和が4である確率を求めよ．

答

事象$A$：ともに3以下の目が出る．
事象$B$：和が3になる．

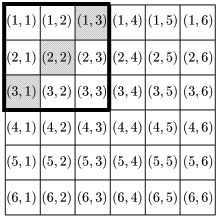
\[\begin{align*} P(A)&=\frac9{36}\\[5pt] P(A\cap B)&=\frac3{36} \end{align*}\]

　よって，

\[P_A(B)=\frac{P(A\cap B)}{P(A)}=\frac{\frac3{36}}{\frac9{36}}=\frac39=\underline{\boldsymbol{\frac13}}\]

補足

　1．事象と確率のところで説明したように，確率を面積で考えるとわかり易い．特に条件付き確率は，面積的な描像があると理解が高まって，ぐっと問題に取り組みやすくなる．

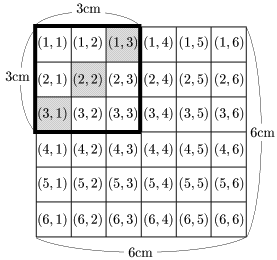
　条件付き確率を面積で考えると，

ともに3以下の目が出る領域 ($3^2=9{\rm cm}^2$)

に占める

和が4となる領域 ($3{\rm cm}^2$)

の割合，即ち $\dfrac39=\dfrac13$ となる．

5.2　確率の乗法定理

　条件付き確率 $P_A(B)=\dfrac{P(A\cap B)}{P(A)}$ の分母を払うと，

\[P(A\cap B)=P(A)P_A(B)\]

という式が得られる．これを確率の乗法定理という．
　$P(A\cap B)$ を求める際，右辺の $P_A(B)$ が容易に計算できる場合などに威力を発揮する．

例　10本中2本が当たりのくじを10人が順番に引くとき，2人目が当たりくじを引く確率．（ただし引いたくじは戻さない．）

　事象A：1人目が当たる
　事象B：2人目が当たる

「1人目も2人目も当たり $(A\cap B)$」と「1人目がはずれ，2人目が当たり $(\overline{A}\cap B)$」 の排反事象に分けて，

\[\begin{align*} P(B)&=P(A\cap B)+P(\overline{A}\cap B)\\[5pt] &=P(A)P_A(B)+P(\overline{A})P_{\bar{A}}(B)\\[5pt] &=\frac2{10}\cdot\frac19+\frac8{10}\cdot\frac29\\[5pt] &=\frac{2+16}{90}\\[5pt] &=\underline{\boldsymbol{\frac15}} \end{align*}\]

※2行目の $P_A(B)$ は，「1人目が当たったという条件の下で2人目が当たりくじを引く確率」，即ち「9本中1本が当たりのくじで，当たりくじを引く確率」を意味する．$P_{\bar{A}}(B)$ も同様．

補足

　$n$ 本中 $a$ 本が当たりのくじ引きで，引いたくじを戻す場合に当たる確率が皆等しく $\dfrac an$ になるのは当然として，引いたくじを戻さない場合であっても，当たりが出る確率は何番目に引く人でも皆同じで $\dfrac an$ となる．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学A　第2章　確率

	スライド	ノート
1. 事象と確率	[無料]
2. 確率の基本性質	[無料]
3. 独立な試行の確率	[会員]
4. 反復試行の確率	[会員]
5. 条件付き確率	[会員]