高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | |
| 1. 放物線 | [会員] | |
| 2. 楕円 | [会員] | |
| 3. 双曲線 | [会員] | |
| 4. 2次曲線の平行移動 | [会員] | |
| 5. 2次曲線と直線 | [会員] | |
| 6. 2次曲線の性質 | [会員] | |
| 7. 曲線の媒介変数表示 | [会員] | |
| 8. 極座標と極方程式 | [会員] |
2．楕円
2.1 楕円の方程式
楕円とは?
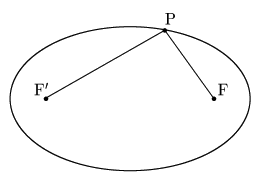
2定点F，F’からの距離の和が一定である点Pの軌跡
2定点F，F’を焦点という．
楕円の方程式
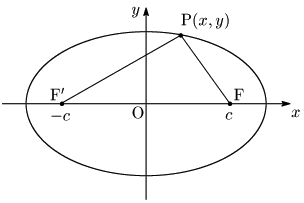
焦点：F$(c,0)$，F’$(-c,0)$
距離の和：$2a$ (ただし，$a>c>0$)
である楕円の方程式を求める．
\[\begin{align*} &{\rm FP+F’P}=2a\ \ \cdots\mbox{①}\\[5pt] \iff &\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a\\[5pt] \iff &\sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}\\[5pt] \Longrightarrow\ &(x-c)^2+y^2=\left(2a-\sqrt{(x+c)^2+y^2}\right)^2\\[5pt] \end{align*}\]
整理して，
\[\begin{align*} &a\sqrt{(x+c)^2+y^2}=a^2+cx\\[5pt] \Longrightarrow\ &a^2\{(x+c)^2+y^2\}=(a^2+cx)^2\\[5pt] \end{align*}\]
よって，
\[(a^2-c^2)x^2+a^2y=a^2(a^2-c^2)\]
ここで，$\sqrt{a^2-c^2}=b$ とおくと，
\[b^2x^2+a^2y^2=a^2b^2\]
$\therefore \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ \ \cdots$ ②
従って条件①を満たす点は，曲線②上にある．逆に曲線②上の任意の点は，$c=\sqrt{a^2-b^2}$ とおくことで条件①を満たす．(詳しくはスライドで．)
方程式②を，楕円の方程式の標準形という．
別の求め方
${\rm FP+F’P}=2a\ \ \cdots\mbox{①}$
一方，
\[\begin{align*} &{\rm FP^2-F’P^2}\\[5pt] =&\{(x-c)^2+y^2\}-\{(x+c)^2+y^2\}\\[5pt] =&-4cx \end{align*}\]
であるから，
\[\begin{align*} {\rm FP^2-F’P^2}&=-4cx\\[5pt] ({\rm FP+F’P})({\rm FP-F’P})&=-4cx\\[5pt] \therefore {\rm FP-F’P}&=-\frac{2cx}a\ \ (\because\mbox{①})\ \ \cdots\ \mbox{②} \end{align*}\]
(①$+$②)$\div$2 より，
\[\begin{align*} {\rm FP}&=a-\frac{cx}a\\[5pt] \therefore {\rm FP^2}&=\left(a-\frac{cx}a\right)^2\\[5pt] (x-c)^2+y^2&=a^2-2cx+\frac{c^2}{a^2}x^2\\[5pt] \frac{a^2-c^2}{a^2}x^2+y^2&=a^2-c^2 \end{align*}\]
$a>c>0$ より，$a^2-c^2>0$ であるから，$b=\sqrt{a^2-c^2}$ とおくと，
\[\begin{align*} \frac{b^2}{a^2}x^2+y^2&=b^2\\[5pt] \therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}&=1 \end{align*}\]
楕円の性質
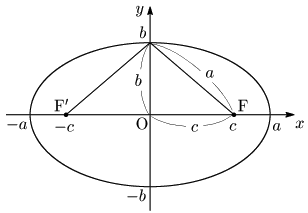
楕円$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (a>b>0)$ において，
- $y=0$ のとき，$x=\pm a$
$x=0$ のとき，$y=\pm b$ - $\sqrt{a^2-c^2}=b$ とおいたから，$c=\pm\sqrt{a^2-b^2}$
楕円の性質
楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ \ (a>b>0)$ において，
① 焦点は $x$ 軸上で，F$(\sqrt{a^2-b^2},0)$，F’$(-\sqrt{a^2-b^2},0)$
② 座標軸との交点(頂点)は
$(a,0),(-a,0),(0,b),(0,-b)$
③ 長軸の長さ $2a$，短軸の長さ $2b$
長軸と短軸の交点(楕円の中心) $(0,0)$
④ $x$ 軸，$y$ 軸，原点に関して対称
⑤ 楕円上の任意の点から焦点までの距離の和は $2a$
例題 楕円 $\dfrac{x^2}9+\dfrac{y^2}4=1$ の焦点，頂点，長軸・短軸の長さ，中心を求めよ．
こたえ
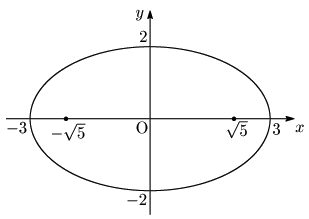
焦点：$\sqrt{9-4}=\sqrt5$ より，$(\sqrt5,0),(-\sqrt5,0)$
頂点：$(3,0),(-3,0),(0,2),(0,-2)$
長軸の長さ：$2\times3=6$，短軸の長さ：$2\times2=4$
中心：$(0,0)$
2.2 焦点が $y$ 軸上にある楕円
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (b>a>0)\ \cdots$① のとき，この曲線を直線 $y=x$ に関して対称移動したグラフをもつ方程式は，
\[\frac{x^2}{b^2}+\frac{y^2}{a^2}=1\ \ (b>a>0)\]
である．これは $(\pm\sqrt{b^2-a^2},0)$ を焦点とし，焦点までの距離の和が $2b$ の楕円であったから，元に戻して考えると，①は焦点 $(0,\sqrt{b^2-a^2}),(0,-\sqrt{b^2-a^2})$ で，距離の和が $2b$ の楕円である．
$y$ 軸上に焦点をもつ楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (b>a>0)$ は，焦点 $(0,\sqrt{b^2-a^2}),(0,-\sqrt{b^2-a^2})$ で，長軸は $y$ 軸上，短軸は $x$ 軸上にある．
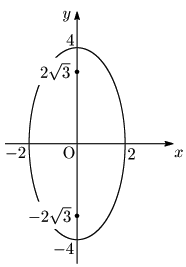
例題 楕円 $\dfrac{x^2}4+\dfrac{y^2}{16}=1$ の焦点，長軸・短軸の長さを求め，グラフをかけ．
こたえ $\sqrt{16-4}=2\sqrt3$ より，焦点 $(0,2\sqrt3),\ (0,-2\sqrt3)$
長軸の長さ：$2\times4=8$，短軸の長さ：$2\times2=4$
2.3 円と楕円
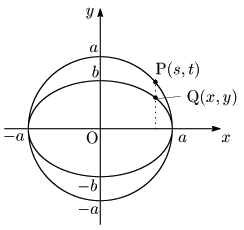
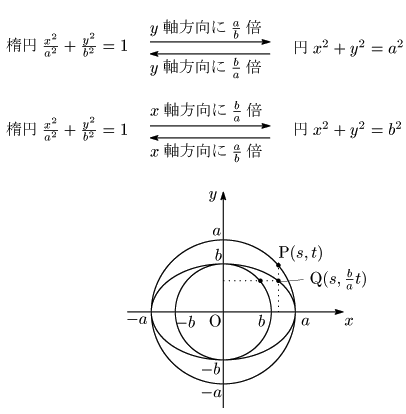
円 $x^2+y^2=a^2$ 上の点を P$(s,t)\ (s^2+t^2=a^2\ \cdots$①)を，$y$ 軸方向に $\dfrac ba$ 倍した点を Q$(x,y)$ とする．
\[\left\{\begin{array}{l} x=s\\ y=\dfrac bat \end{array}\right. \ \ \therefore \left\{ \begin{array}{l} s=x\\ t=\dfrac aby \end{array}\right.\]
これらを①に代入して
\[\begin{align*} x^2+\left(\frac aby\right)^2&=a^2\\[5pt] \therefore\ \frac{x^2}{a^2}+\frac{y^2}{b^2}&=1 \end{align*}\]
よって，点Qの軌跡は，楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
