高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | |
| 1. 放物線 | [会員] | |
| 2. 楕円 | [会員] | |
| 3. 双曲線 | [会員] | |
| 4. 2次曲線の平行移動 | [会員] | |
| 5. 2次曲線と直線 | [会員] | |
| 6. 2次曲線の性質 | [会員] | |
| 7. 曲線の媒介変数表示 | [会員] | |
| 8. 極座標と極方程式 | [会員] |
3.双曲線
3.1 双曲線の方程式
双曲線とは?
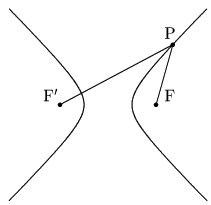
2定点F,F’からの距離の差が一定である点Pの軌跡
2定点F,F’を焦点という.
双曲線の方程式
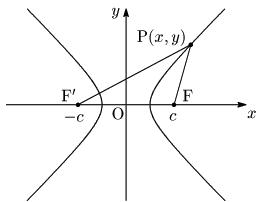
焦点:F$(c,0)$,F’$(-c,0)$
距離の差:$2a$ (ただし,$c>a>0$)
である双曲線の方程式を求める.
\[\begin{align*} &|{\rm FP-F’P}|=2a\ \ \cdots\mbox{①}\\[5pt] \iff &{\rm FP-F’P}=\pm 2a\\[5pt] \iff &{\rm FP}={\rm F’P}\pm 2a\\[5pt] \Longrightarrow\ &{\rm FP}^2={\rm F’P}^2\pm 4a\cdot{\rm F’P}+4a^2\\[5pt] \iff &(x\!-\!c)^2\!+\!y^2\!=\!(x\!+\!c)^2\!+\!y^2\!\pm\! 4a\sqrt{(x\!+\!c)^2\!+\!y^2}\!+\!4a^2\\[5pt] \iff &\pm a\sqrt{(x+c)^2+y^2}=a^2+cx\\[5pt] \iff &a^2\{(x+c)^2+y^2\}=(a^2+cx)^2\\[5pt] \iff &(c^2-a^2)x^2-a^2y^2=a^2(c^2-a^2) \end{align*}\]
ここで $\sqrt{c^2-a^2}=b$ とおくと,
\[\begin{align*} b^2x^2-a^2y^2&=a^2b^2\\[5pt] \therefore\ \frac{x^2}{a^2}-\frac{y^2}{b^2}&=1\ \ \cdots\mbox{②} \end{align*}\]
よって条件①を満たす点は,曲線②上にある.逆に曲線②上の任意の点は,$c=\sqrt{a^2+b^2}$ とおくことで条件①を満たす.(詳しくはスライドで.)
方程式②を,双曲線の方程式の標準形という.
直線FF’と双曲線の2つの交点を頂点,線分FF’の中点を双曲線の中心という.
双曲線は,$x$ 軸,$y$ 軸,原点に関して対称である.
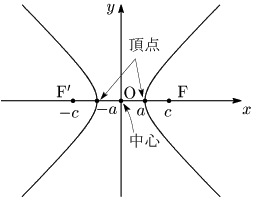
補足
双曲線においては,$a,b$ の大小関係を考えなくてよい.
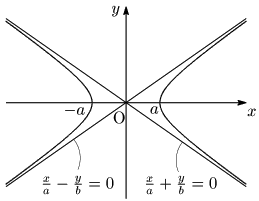
双曲線の漸近線
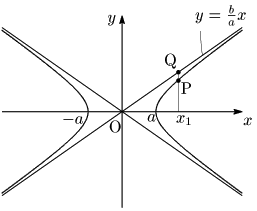
$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\ \cdots$①より
\[y^2=\frac{b^2}{a^2}(x^2-a^2)\]
今,$x>0,y>0$ の場合を考えると,
\[y=\frac ba\sqrt{x^2-a^2}\]
となる.ここで,直線 $y=\dfrac bax$ との差(図のPQ)を考えると,
\[\begin{align*} {\rm PQ}&=\frac bax_1-\frac ba\sqrt{{x_1}^2-a^2}\\[5pt] &=\frac ba(x_1-\sqrt{{x_1}^2-a^2})\\[5pt] &=\frac ba\cdot\frac{(x_1-\sqrt{{x_1}^2-a^2})(x_1+\sqrt{{x_1}^2-a^2})}{(x_1+\sqrt{{x_1}^2-a^2})}\\[5pt] &=\frac ba\cdot\frac{a^2}{(x_1+\sqrt{{x_1}^2-a^2})}\\[5pt] &=\frac{ab}{(x_1+\sqrt{{x_1}^2-a^2})}\\[5pt] &\to 0\ (x_1\to\infty) \end{align*}\]
となるから,第1象限で $y=\dfrac bax$ は漸近線となる.
①は原点に関して対称であるから,$y=\dfrac bax$ は第3象限でにおいても漸近線である.
また,①は $y$ 軸に関しても対称であるから,$y=-\dfrac bax$ も①の漸近線である.
補足
① 漸近線の方程式は,双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ の右辺を0とおいた,$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=0$,即ち
\[\left(\dfrac xa+\dfrac yb\right)\left(\dfrac xa-\dfrac yb\right)=0\]
の表す2直線である.
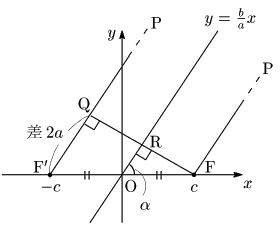
② 双曲線上の点Pが第1象限の無限遠方にある場合は,図でほぼ ${\rm PF\,/\!/\,PF’}$ となるから,焦点までの距離の差が ${\rm F’Q}=2a$ より ${\rm OR}=\dfrac12{\rm F’Q}=a$.また,$\tan\alpha=\dfrac ba$ より,${\rm FR}={\rm OR}\tan\alpha=b$.よって,△OFRにおいて,$c=\sqrt{a^2+b^2}$.
③ 直交する漸近線をもつ双曲線を,直角双曲線という.
例 $x^2-y^2=1$ (漸近線:$x\pm y=0$)
双曲線の性質
双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\ \ (a>0,\ b>0)$ において,
① 焦点は $x$ 軸上で,F$(\sqrt{a^2+b^2},0)$,F’$(-\sqrt{a^2+b^2},0)$
中心(線分 $\rm FF’$ の中点)は $(0,0)$
② 座標軸との交点(頂点)は $(a,0),\ (-a,0)$
③ $x$ 軸,$y$ 軸,原点に関して対称
④ 漸近線は,2直線 $\dfrac xa-\dfrac yb=0,\ \dfrac xa+\dfrac yb=0$
⑤ 楕円上の任意の点から焦点までの距離の差は $2a$
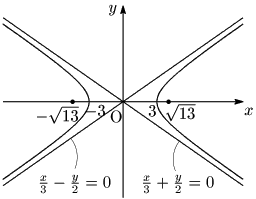
例題 双曲線 $\dfrac{x^2}9-\dfrac{y^2}4=1$ の焦点,頂点,漸近線の方程式を求め,グラフをかけ.漸近線もかくこと.
こたえ
焦点:$\sqrt{9+4}=\sqrt{13}$ より,$(\sqrt{13},0),(-\sqrt{13},0)$
頂点:$(3,0),(-3,0)$
漸近線:$\dfrac x3-\dfrac y2=0,\dfrac x3+\dfrac y2=0$
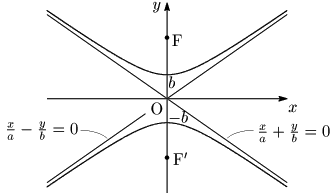
3.2 焦点が $y$ 軸上にある双曲線
曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1\ (a>0,b>0)\ \cdots$① を,直線 $y=x$ に関して対称移動すると,
\[\frac{y^2}{a^2}-\frac{x^2}{b^2}=-1\ \therefore \frac{x^2}{b^2}-\frac{y^2}{a^2}=1\]
これは双曲線の方程式で,
焦点 :F$(\sqrt{a^2+b^2},0)$,F’$(-\sqrt{a^2+b^2},0)$
頂点 :$(b,0),\ (-b,0)$
漸近線:$\dfrac xb-\dfrac ya=0,\ \dfrac xb+\dfrac ya=0$
であったから,対称移動前を考えると①は次のような双曲線であることがわかる:
焦点 :F$(0,\sqrt{a^2+b^2})$,F’$(0,-\sqrt{a^2+b^2})$
頂点 :$(0,b),\ (0,-b)$
漸近線:$\dfrac xa-\dfrac yb=0,\ \dfrac xa+\dfrac yb=0$
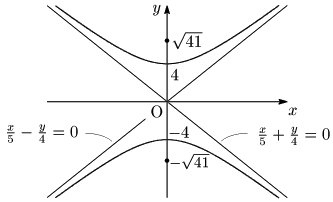
例題 双曲線 $\dfrac{x^2}{25}-\dfrac{y^2}{16}=-1$ の焦点,頂点,漸近線を求め,グラフをかけ.漸近線もかくこと.
こたえ
焦点:$\sqrt{25+16}=\sqrt{41}$ より,$(0,\sqrt{41}),(0,-\sqrt{41})$
頂点:$(0,4),(0,-4)$
漸近線:$\dfrac x5-\dfrac y4=0,\dfrac x5+\dfrac y4=0$
このページで疑問は解決されましたか?
こちらから数学に関するご質問・ご要望をお寄せください。
