6．2次曲線の性質(ノート)｜スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第5章　2次曲線

	スライド	ノート
1. 放物線	[会員]
2. 楕円	[会員]
3. 双曲線	[会員]
4. 2次曲線の平行移動	[会員]
5. 2次曲線と直線	[会員]
6. 2次曲線の性質	[会員]
7. 曲線の媒介変数表示	[会員]
8. 極座標と極方程式	[会員]

6．2次曲線の性質

　放物線，楕円，双曲線の3つの曲線は，

• 放物線：定点と定直線から等距離にある点の軌跡
• 楕円：2点からの距離の和が一定である点の軌跡
• 双曲線：2点からの距離の差が一定である点の軌跡

として導入された．実はこれら2次曲線はもう少し統一した形でも導入することができる．それは以下に示す離心率と呼ばれる比率を用いた方法だ．

6.1 離心率

　原点Oを通らない定直線 $\ell$ を $x=k$，点P$(x,y)$ から $\ell$ に下ろした垂線の足をHとする． OP：PH$=e:1$ $(e>0)$ となる点Pの軌跡を考えよう．

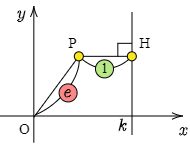
\[\begin{align*} &{\rm OP:PH}=e:1\\[5pt] \iff& {\rm OP}=e{\rm PH}\\[5pt] \iff& \sqrt{x^2+y^2}=e|x-k|\\[5pt] \iff& x^2+y^2=e^2(x-k)^2\\[5pt] \iff& (1-e^2)x^2+y^2+2e^2kx-e^2k^2=0 \end{align*}\]

　従って

• $0<e<1$ のとき
  $x^2$ と $y^2$ の係数が同符号になるから楕円
  （もちろんこのとき $-2e^2kx+e^2k^2>0$ となることは必要）
• $e=1$ のとき
  $x^2$ の項が落ちるから放物線
• $e>1$ のとき
  $x^2$ と $y^2$ の係数が異符号になるから双曲線

となることがわかる．（$x^2$ と $y^2$ の項以外は概形を決定付けない．）

　一般に，定点Fと，Fを通らない直線 $\ell$ からの距離の比が FP：PH$=e:1$ $(e>0)$ となる点Pの軌跡は次のようになる：

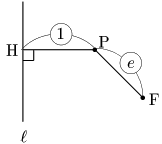
　$e$ の値を2次曲線の離心率(eccentricity)，直線 $\ell$ を準線という．

例題　原点Oと直線 $x=3$ からの距離の比が一定で，$e:1$ である点Pの軌跡 $C$ を，
　　[1] $e=\dfrac12$　[2] $e=1$　[3] $e=2$
の各場合について求めよ．

こたえ

　${\rm OP:PH}=e:1$ より，${\rm OP}=e{\rm PH}$

　両辺を2乗して　${\rm OP}^2=e^2{\rm PH}^2$

　よって　　$x^2+y^2=e^2|x-3|^2$

　整理して　$(1-e^2)x^2+y^2+6e^2x-9e^2=0\ \cdots$①

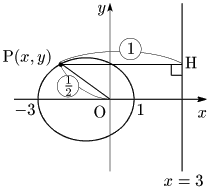
[1] $e=\dfrac12$ のとき

　　①に代入して整理すると　$\dfrac{(x+1)^2}4+\dfrac{y^2}3=1$

　　よって $C$ は楕円 $\dfrac{x^2}4+\dfrac{y^2}3=1$ を $x$ 軸方向に $-1$ だけ平行移動した楕円．

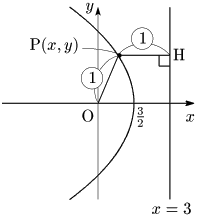
[2] $e=1$ のとき

　　①に代入して整理すると　$y^2=-6\left(x-\dfrac32\right)$

　　よって $C$ は放物線 $y^2=-6x$ を $x$ 軸方向に $\dfrac32$ だけ平行移動した放物線．

[3] $e=2$ のとき

　　①に代入して整理すると　$\dfrac{(x-4)^2}4-\dfrac{y^2}{12}=1$

　　よって $C$ は双曲線 $\dfrac{x^2}4-\dfrac{y^2}{12}=1$ を $x$ 軸方向に $4$ だけ平行移動した双曲線．

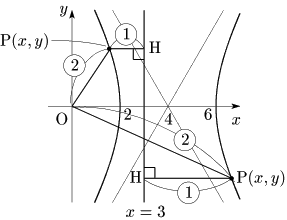
補足

　双曲線は2つの曲線が対になっているが，すぐ上の図を見ればわかるように1つの焦点と対応する準線1本で2つの曲線が共に描かれる．

6.2 標準形と離心率

　標準形で与えられた2次曲線に対して，その離心率と準線はどのように表されるのだろうか。放物線 $y^2=4px$ は離心率が1，準線が直線 $x=-p$ とすぐにわかるからよいとして，問題は楕円と双曲線である．これらの場合を以下で調べるのであるが，いずれの場合も

焦点と曲線上の点の距離を計算すると，その結果に離心率と準線が自然と現れる

というのがポイントである．ついでに述べておくと，2点間の距離を計算する際に現れる根号は外れないことも多いが，標準形で表された2次曲線の場合は中身が平方式になって根号が外れることもぜひ覚えておきたい．

楕円

　楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (a>b>0)$ 上の点をP$(x,y)$，焦点の1つをF$(c,0)$ とする．$(c=\sqrt{a^2-b^2})$

\[\begin{align} {\rm FP}&=\sqrt{(x-c)^2+y^2}\\[5pt] &=\sqrt{(x^2-2cx+c^2)+\left(-\frac {b^2}{a^2}x^2+b^2\right)}\\[5pt] &=\sqrt{\frac{a^2-b^2}{a^2}x^2-2cx+(b^2+c^2)}\\[5pt] &=\sqrt{\frac{c^2}{a^2}x^2-2cx+a^2}\ \ (\because c=\sqrt{a^2-b^2})\\[5pt] &=\sqrt{\left(\frac cax-a\right)^2}\\[5pt] &=\left|\frac cax-a\right|\\[5pt] &=\frac ca\left|x-\frac{a^2}c\right| \end{align}\]

　よって，直線 $\ell$ を $x=\dfrac{a^2}c$ とし，Pから $\ell$ に下ろした垂線の足をHとすると，

\[{\rm FP}=\dfrac ca{\rm PH}\]

\[\therefore {\rm FP:PH}=\frac ca:1\]

　従って離心率 $e=\dfrac ca=\dfrac{\sqrt{a^2-b^2}}a$ である．

　またこのときの $e$ を用いると，$c=ae$ より

　　　準線 $\ell:x=\dfrac{a^2}c=\dfrac ae$
　　　焦点：$(ae,0)$

となる．また対称性により，

　　　準線 $\ell:x=-\dfrac{a^2}c=-\dfrac ae$
　　　焦点：$(-ae,0)$

の組もある．

まとめ 　楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (a>b>0)$ において，
　　離心率　$e=\dfrac{\sqrt{a^2-b^2}}a$
　　焦点　　$(\pm ae,0)$
　　準線　　$x=\pm\dfrac ae$
　　(複号同順)

双曲線

　双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\ (a>0,b>0)$ 上の点をP$(x,y)$，焦点の1つをF$(c,0)$ とする．$(c=\sqrt{a^2+b^2})$

\[\begin{align} {\rm FP}&=\sqrt{(x-c)^2+y^2}\\[5pt] &=\sqrt{(x^2-2cx+c^2)+\left(\frac {b^2}{a^2}x^2-b^2\right)}\\[5pt] &=\sqrt{\frac{a^2+b^2}{a^2}x^2-2cx+(c^2-b^2)}\\[5pt] &=\sqrt{\frac{c^2}{a^2}x^2-2cx+a^2}\ \ (\because c=\sqrt{a^2+b^2})\\[5pt] &=\sqrt{\left(\frac cax-a\right)^2}\\[5pt] &=\left|\frac cax-a\right|\\[5pt] &=\frac ca\left|x-\frac{a^2}c\right| \end{align}\]

　従って離心率 $e=\dfrac ca=\dfrac{\sqrt{a^2+b^2}}a$ である．

　またこのときの $e$ を用いると，$c=ae$ より

　　　準線 $\ell:x=\dfrac{a^2}c=\dfrac ae$
　　　焦点：$(ae,0)$

となる．また対称性により

　　　準線 $\ell:x=-\dfrac{a^2}c=-\dfrac ae$
　　　焦点：$(-ae,0)$

の組もある．

まとめ 　双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\ (a>0,b>0)$ において，
　　離心率　$e=\dfrac{\sqrt{a^2+b^2}}a$
　　焦点　　$(\pm ae,0)$
　　準線　　$x=\pm\dfrac ae$
　　(複号同順)