7．曲線の媒介変数表示(ノート)｜スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第5章　2次曲線

	スライド	ノート
1. 放物線	[会員]
2. 楕円	[会員]
3. 双曲線	[会員]
4. 2次曲線の平行移動	[会員]
5. 2次曲線と直線	[会員]
6. 2次曲線の性質	[会員]
7. 曲線の媒介変数表示	[会員]
8. 極座標と極方程式	[会員]

7．曲線の媒介変数表示

7.1 媒介変数表示

　平面上の曲線 $C$ が，変数 $t$ によって

\[x=f(t),\ y=g(t)\]

の形に表されるとき，これを曲線 $C$ の媒介変数表示，またはパラメータ表示という．また，変数$t$を媒介変数，またはパラメータという．

例題　$x=t-1,\ y=t^2-2t$ で表される図形 $C$ はどのようなものか．

こたえ

　解答例を表示する >

　$x=t-1$ より $t=x+1$．これを $y$ の式に代入して

\[y=(x+1)^2-2(x+1)=x^2-1\]

　よって，$C$ は放物線 $y=x^2-1$．

7.2 放物線の媒介変数表示

　$y^2=4px\ (\cdots$①) より　$x=\dfrac{y^2}{4p}$．

　よって，$t$ を実数として $y=2pt$ とおくと，$y$ は実数全体をとり，$x=pt^2$．従って①の媒介変数表示の１つは

\[(pt^2,\ 2pt)\]

放物線 $y^2=4px$ の媒介変数表示 \[(pt^2,\ 2pt)\]

例題　$y^2=4x$ について，上と同様の媒介変数表示をせよ．

こたえ

　解答例を表示する >

　$y^2=4\cdot1x$より$p=1$．よって，$(t^2,2t)$

7.3 円の媒介変数表示

　原点Oを中心とする円 $x^2+y^2=a^2\ (\cdots$①) 上の点をP$(x,y)$ とし，動径OPの表す一般角を $\theta$ とすると，三角関数の定義から

\[x=a\cos\theta,\ y=a\sin\theta\]

　これは，円①の媒介変数表示となっている．

円 $x^2+y^2=a^2$ の媒介変数表示 \[(a\cos\theta,\ a\sin\theta)\]

例題　円 $x^2+y^2=4$ について，上と同様の媒介変数表示をせよ．

こたえ

　解答例を表示する >

　$(2\cos\theta,\ 2\sin\theta)$

7.4 楕円の媒介変数表示

　楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\ (\cdots$①) 上の点 $(x,y)$ に対し，

\[X=\frac xa,\ Y=\frac yb\]

とおくと，①は

\[X^2+Y^2=1\]

と表される．これは点 $(X,Y)$ が円 $x^2+y^2=1$ 上の点であることを意味するから，すぐ上で学習したように原点を中心とする半径1の円の媒介変数表示から

\[X=\cos\theta,\ Y=\sin\theta\]

と表せる．よって $\dfrac xa=\cos\theta,\ \dfrac yb=\sin\theta$ より，

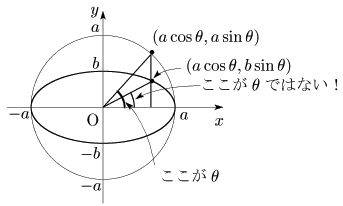
\[x=a\cos\theta,\ y=b\sin\theta\]

楕円 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ の媒介変数表示 \[(a\cos\theta,\ b\sin\theta)\]

例題　楕円 $\dfrac{x^2}{16}+\dfrac{y^2}4=1$ について，上と同様の媒介変数表示をせよ．

こたえ

　解答例を表示する >

　$(4\cos\theta,\ 2\sin\theta)$

重要な注意

　$\theta$ の位置に注意すること．

7.5 双曲線の媒介変数表示

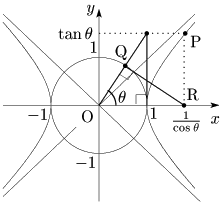
　三角関数の公式より，

\[1+\tan^2\theta=\frac1{\cos^2\theta}\]

$\therefore \dfrac1{\cos^2\theta}-\tan^2\theta=1$

　よって，点 $\left(\dfrac1{\cos\theta},\tan\theta\right)\ \ \cdots$① は，双曲線 $x^2-y^2=1$ 上にある．

　一方，単位円周上の点 ${\rm Q}(\cos\theta,\sin\theta)$ に対して，上の図のように点Pをとると，Pの座標は①で表される．

　Pの位置は $\theta$ によって次のようになる：

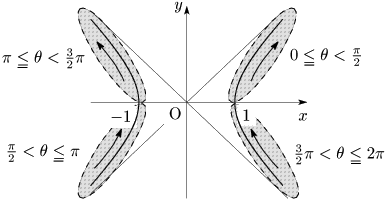
　双曲線 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ で，$X=\dfrac xa,\ Y=\dfrac yb$ とおくと，$X^2-Y^2=1$．よって，点 $(X,Y)$ は①で表されるから，$\dfrac xa=\dfrac1{\cos\theta},\ \dfrac yb=\tan\theta$ より

\[(x,y)=\left(\frac a{\cos\theta},\ b\tan\theta\right)\]

双曲線 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ の媒介変数表示 \[\left(\dfrac a{\cos\theta},\ b\tan\theta\right)\]

例題　双曲線 $\dfrac{x^2}9-\dfrac{y^2}4=1$ について，上と同様の媒介変数表示をせよ．

こたえ

　解答例を表示する >

　$\left(\dfrac 3{\cos\theta},\ 2\tan\theta\right)$

7.6 媒介変数で表された曲線の平行移動

　曲線 $x=f(t),\ y=g(t)$ を、$x$ 軸方向に $p$，$y$ 軸方向に $q$ だけ平行移動した曲線の媒介変数表示は \[x=f(t)+p,\ y=g(t)+q\]

例題　$x=2\cos\theta+3,\ y=2\sin\theta+1$ で表される曲線はどのようなものか．

こたえ

　解答例を表示する >

　$x=2\cos\theta+3,\ y=2\sin\theta+1$ より

\[\cos\theta=\frac{x-3}2,\ \sin\theta=\frac{y-1}2\]

　$\cos^2\theta+\sin^2\theta=1$ に代入して，

\[\left(\frac{x-3}2\right)^2+\left(\frac{y-1}2\right)^2=1\]

　よって　$(x-3)^2+(y-1)^2=4$

　従って点 $(3,1)$ を中心とする半径2の円．

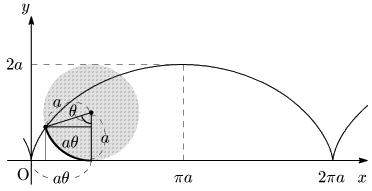
7.7 サイクロイド

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学Ⅲ　第5章　2次曲線

	スライド	ノート
1. 放物線	[会員]
2. 楕円	[会員]
3. 双曲線	[会員]
4. 2次曲線の平行移動	[会員]
5. 2次曲線と直線	[会員]
6. 2次曲線の性質	[会員]
7. 曲線の媒介変数表示	[会員]
8. 極座標と極方程式	[会員]